题目内容
【题目】(本题10分)如图,已知二次函数![]() 的图象的顶点为A,二次函数
的图象的顶点为A,二次函数![]() 的图象与
的图象与![]() 轴交于原点O及另一点C,它的顶点B在函数
轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1) 求点A与点C的坐标;
(2) 当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.

【答案】(1)A的坐标为(1,﹣2),C的坐标为(2,0).
(2)二次函数y=ax2+bx的关系式为y=﹣2x2+4x.
【解析】试题分析:(1)二次函数y=ax2+bx的顶点在已知二次函数抛物线的对称轴上,可知两个函数对称轴相等,因此先根据已知函数求出对称轴.根据函数解析式得出顶点A的坐标与对称轴,故可得出二次函数y=ax2+bx关于x=1对称,且函数与x轴的交点分别是原点和C点,所以点C和点O关于直线l对称,故可得出点C的坐标;
(2)因为四边形AOBC是菱形,根据菱形性质,可以得出点O和点C关于直线AB对称,点B和点A关于直线OC对称,因此,可求出点B的坐标,根据二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),将B,C代入解析式得出ab的值,进而得出其解析式.
试题解析:(1)∵y=x2-2x-1=(x-1)2-2,
∴顶点A的坐标为(1,-2).
∵二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
∴二次函数y=ax2+bx的对称轴为:直线x=1,
∴点C和点O关于直线x=1对称,
∴点C的坐标为(2,0).
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,
因此,点B的坐标为(1,2).
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以![]()
解得![]() ,
,
所以二次函数y=ax2+bx的关系式为y=-2x2+4x.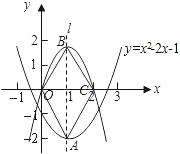

练习册系列答案
相关题目