题目内容
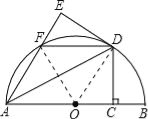
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.

【答案】(1)证明见解析(2)四边形ODFA是菱形
【解析】
试题分析:(1)连接OD,由等腰三角形的性质可得到∠OAD=∠ODA,由图形翻折变换的性质可得到∠CDA=∠EDA,再根据CD⊥AB即可得出结论;
(2)连接OF,可知OC=BC=![]() OB=
OB=![]() OD,由平行线的判定定理可得出OD∥AF,进而可得出△FAO是等边三角形,由等边三角形的性质可判断出四边形ODFA是平行四边形,由OA=OD即可得出结论.
OD,由平行线的判定定理可得出OD∥AF,进而可得出△FAO是等边三角形,由等边三角形的性质可判断出四边形ODFA是平行四边形,由OA=OD即可得出结论.
试题解析:(1)如图,连接OD,则OA=OD,
∴∠OAD=∠ODA,
∵△AED由△ACD对折得到,
∴∠CDA=∠EDA,
又∵CD⊥AB,
∴∠CAD+∠CDA=∠ODA+∠EDA=90°,D点在半圆O上,
∴DE是半圆的切线;
(2)四边形ODFA是菱形,
如图,连接OF,
∵CD⊥OB,
∴△OCD是直角三角形,
∴OC=BC=![]() OB=
OB=![]() OD,
OD,
在Rt△OCD中,∠ODC=30°,
∴∠DOC=60°,
∵∠DOC=∠OAD+∠ODA,
∴∠OAD=∠ODA=∠FAD=30°,
∴OD∥AF,∠FAO=60°,
又∵OF=OA,
∴△FAO是等边三角形,
∴OA=AF,
∴OD=AF,
∴四边形ODFA是平行四边形,
∵OA=OD,
∴四边形ODFA是菱形.

【题目】2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人.如表是苏炳添近五次大赛参赛情况:
比赛日期 | 2012-8-4 | 2013-5-21 | 2014-9-28 | 2015-5-20 | 2015-5-31 |
比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
则苏炳添这五次比赛成绩的众数和平均数分别为( )
A.10.06秒,10.06秒 B.10.10秒,10.06秒
C.10.06秒,10.08秒 D.10.08秒,10.06秒