题目内容
【题目】已知,如图,CD⊥AB,GF⊥AB,∠B=∠ADE,试说明∠1=∠2. 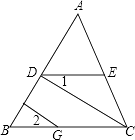
【答案】证明:∵∠B=∠ADE(已知), ∴DE∥BC(同位角相等,两直线平行)
∴∠1=∠DCB.(两直线平行,内错角相等)
∵CD⊥AB,GF⊥AB,
∴CD∥FG(平面内,垂直于同一条直线的两条直线平行),
∴∠2=∠DCB.(两直线平行,同位角相等)
∴∠1=∠2.(等量代换)
【解析】利用平行线的判定及性质,通过证明∠1=∠BCD=∠2达到目的.
【考点精析】本题主要考查了垂线的性质和平行线的判定与性质的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
相关题目
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.