题目内容
【题目】在△ABC中,AB=AC=2,∠BAC=45°.将△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,B,C两点的对应点分别为点D,E,BD,CE所在直线交于点F.
(1)当△ABC旋转到图1位置时,∠CAD= (用α的代数式表示),∠BFC的度数为 °;
(2)当α=45时,在图2中画出△ADE,并求此时点A到直线BE的距离.

【答案】(1)α﹣45°,45°;(2)图详见解析,点A到直线BE的距离为![]() .
.
【解析】
(1)如图1,利用旋转的性质得∠BAD=∠CAE=α,AB=AD,AE=AC,则∠CAD=α﹣45°;再利用等腰三角形的性质和三角形内角和得到∠ABD=∠ACE,所以∠BFC=∠BAC=45°.
(2)如图2,△ADE为所作,BE与AC相交于G,利用旋转的性质得点D与点C重合,∠CAE=45°,AE=AB=2,则△ABE为等腰直角三角形,所以BE=![]() AB=2
AB=2![]() ,再证明AG⊥BE,然后根据等腰直角三角形的性质求出AG的长即可.
,再证明AG⊥BE,然后根据等腰直角三角形的性质求出AG的长即可.
解:(1)∵△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,如图1,
∴∠BAD=∠CAE=α,AB=AD,AE=AC,
而∠BAC=45°,
∴∠CAD=α﹣45°;
∵AB=AD,AE=AC,
∴∠ABD=∠ADB=![]() (180°﹣∠BAD)=
(180°﹣∠BAD)=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,∠ACE=∠AEC=
α,∠ACE=∠AEC=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴∠ABD=∠ACE,
∴∠BFC=∠BAC=45°.
故答案为α﹣45°;45°;
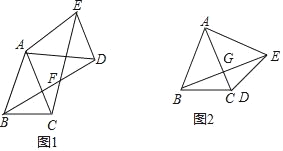
(2)如图2,△ADE为所作,BE与AC相交于G,
∵△ABC绕点A逆时针旋转45度得到△ADE,
而AB=AC,∠BAC=45°,
∴点D与点C重合,∠CAE=45°,AE=AB=2,
∴△ABE为等腰直角三角形,
∴BE=![]() AB=2
AB=2![]() ,
,
而AG平分∠BAE,
∴AG⊥BE,
∴AG=![]() BE=
BE=![]() ,
,
即此时点A到直线BE的距离为![]() .
.