Question

【题目】在正方形ABCD中，点E是AD的中点，连接BE，BF平分∠EBC交CD于点F，交AC于点G，将△CGF沿直线GF折叠至△C′GF，BD与△C′GF相交于点M、N，连接CN，若AB=6，则四边形CNC′G的面积是_____．

Answer 1

【答案】24﹣48

【解析】

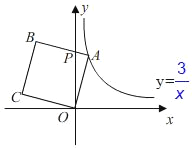
建立如图坐标系，延长BE交CD的延长线于K．则易知AB＝DK＝6，CK＝12，BE＝EK＝3，BK＝6．利用角平分线的性质定理，求出CF，点G的坐标，再求出C′F的解析式，利用方程组求出点N的坐标，即可解决问题．

建立如图坐标系，延长BE交CD的延长线于K．则易知AB＝DK＝6，CK＝12，BE＝EK＝3，BK＝6．

∵BF平分∠CBK，

∴，

CF＝3（1），F[6，3（1）]．

∵CG平分∠ACF，

∴可得CG＝93，S△CGF＝CGCFsin45°＝1836，

由C′（，），F[6，3（-1）]，

∴直线C′F的解析式为y＝x＋3，

由，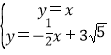

解得N（2，2），

∴S△CFN＝（62）3（1）＝1224，

∴S四边形CNC′G＝2S△CFGS△CFN＝367212＋24＝2448．

故答案为：2448．