Question

已知△ABC中，D，E两点在BC上，AB=AC，AD=AE，你能判断BD与EC的大小关系吗？试说明理由．

Answer 1

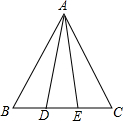解：BD=EC
理由如下：∵AD=AE
∴∠ADE=∠AED
∵AB=AC
∴∠B=∠C
∴∠BAD=∠ADE-∠B=∠AED-∠C=∠CAE
又∵AB=AC，AD=AE
∴△ABD≌△ACE
∴BD=EC．
分析：相等，可通过全等三角形来证得，三角形ABD和AEC中，AB=AC，AD=AE，我们只要再证得两组对应边的夹角相等即可，可通过三角形ABD，AEC的外角相等且∠B=∠C来证得∠BAD=∠EAC，由此可得出两三角形全等从而得出BD=EC．
点评：本题考查了全等三角形的判定，通过全等三角形得出简单的线段相等是解题的关键．