题目内容
当k=1,2,3,…,2004,2005时,求所有函数y=k(k+1)x2-(2k+1)x+1的图象在x轴上所截得的线段长度的和.
解:设y=k(k+1)x2-(2k+1)x+1与x轴的交点坐标为(x1,O)、(x2,O),
∴|x1-x2|= =
= ,
,
而k为正整数,
∴|x1-x2|= =
= -
- ,
,
∴当k=1,2,3,…,2004,2005,
所有函数y=k(k+1)x2-(2k+1)x+1的图象在x轴上所截得的线段长度的和
=(1- )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+( -
- )
)
=1-
= .
.
分析:设y=k(k+1)x2-(2k+1)x+1与x轴的交点坐标为(x1,O)、(x2,O),根据抛物线与x轴两交点的距离公式得到|x1-x2|= =
= ,根据k为正整数变形为|x1-x2|=
,根据k为正整数变形为|x1-x2|= =
= -
- ,然后把k=1,2,3,…,2004,2005代入计算即可得到所有线段长度的和.
,然后把k=1,2,3,…,2004,2005代入计算即可得到所有线段长度的和.
点评:本题考查了抛物线y=ax2+bx+c(a≠0)与x轴两交点的距离公式:设y=ax2+bx+c(a≠0)与x轴的交点坐标为(x1,O)、(x2,O),则|x1-x2|=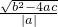 (b2-4ac>0).也考查了分数的运算技巧.
(b2-4ac>0).也考查了分数的运算技巧.
∴|x1-x2|=
 =
= ,
,而k为正整数,
∴|x1-x2|=
 =
= -
- ,
,∴当k=1,2,3,…,2004,2005,
所有函数y=k(k+1)x2-(2k+1)x+1的图象在x轴上所截得的线段长度的和
=(1-
 )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+( -
- )
)=1-

=
 .
.分析:设y=k(k+1)x2-(2k+1)x+1与x轴的交点坐标为(x1,O)、(x2,O),根据抛物线与x轴两交点的距离公式得到|x1-x2|=
 =
= ,根据k为正整数变形为|x1-x2|=
,根据k为正整数变形为|x1-x2|= =
= -
- ,然后把k=1,2,3,…,2004,2005代入计算即可得到所有线段长度的和.
,然后把k=1,2,3,…,2004,2005代入计算即可得到所有线段长度的和.点评:本题考查了抛物线y=ax2+bx+c(a≠0)与x轴两交点的距离公式:设y=ax2+bx+c(a≠0)与x轴的交点坐标为(x1,O)、(x2,O),则|x1-x2|=
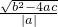 (b2-4ac>0).也考查了分数的运算技巧.
(b2-4ac>0).也考查了分数的运算技巧. 
练习册系列答案
相关题目
 如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s). 水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.
水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象. ?试写出你的猜想,并说明理由.
?试写出你的猜想,并说明理由.