��Ŀ����
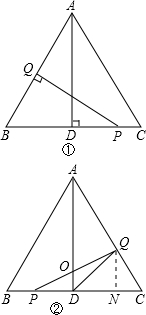
 ��ͼ���ڡ�ABC�У���֪AB=BC=CA=4cm��AD��BC��D����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s����
��ͼ���ڡ�ABC�У���֪AB=BC=CA=4cm��AD��BC��D����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s������1����x=
��2�����PQD�����Ϊy��cm2������0��x��2ʱ����y��x�ĺ�����ϵʽΪ
��3����0��x��2ʱ����֤��ADƽ�֡�PQD�������
��4��̽����PQΪֱ����Բ��AC��λ�ù�ϵ����д����Ӧλ�ù�ϵ��x��ȡֵ��Χ����Ҫ��д�����̣���
��������1����ʹPQ��AC�������·��=�ٶȡ�ʱ���ʾ��CP��CQ�ij����ٸ���30�ȵ�ֱ�������ε������з�����⣻
��ʹPQ��AB�������·��=�ٶȡ�ʱ���ʾ��BP��BQ�ij����ٸ���30�ȵ�ֱ�������ε������з�����⣻
��2�����Ȼ������������ͼ�Σ��ٸ���·��=�ٶȡ�ʱ���ʾ��BP��CQ�ij������ݵȱ������ε����ߺ�һ���PD�ij�������30�ȵ�ֱ�������ε��������PD���ϵĸߣ��ٸ��������ʽ������⣻
��3�����������ε������ʽ��Ҫ֤��ADƽ�֡�PQD�������ֻ��֤��O��PQ���е㣮�����������֤��BP=CN����PD=DN���ٸ���ƽ���ߵȷ��߶ζ�������֤����
��4�����ݣ�1������õ�ֵ���ɷ�����������ۣ�
��ʹPQ��AB�������·��=�ٶȡ�ʱ���ʾ��BP��BQ�ij����ٸ���30�ȵ�ֱ�������ε������з�����⣻
��2�����Ȼ������������ͼ�Σ��ٸ���·��=�ٶȡ�ʱ���ʾ��BP��CQ�ij������ݵȱ������ε����ߺ�һ���PD�ij�������30�ȵ�ֱ�������ε��������PD���ϵĸߣ��ٸ��������ʽ������⣻
��3�����������ε������ʽ��Ҫ֤��ADƽ�֡�PQD�������ֻ��֤��O��PQ���е㣮�����������֤��BP=CN����PD=DN���ٸ���ƽ���ߵȷ��߶ζ�������֤����
��4�����ݣ�1������õ�ֵ���ɷ�����������ۣ�
��� �⣺��1��
�⣺��1��
��
��
��Q��AB��ʱ����ȻPQ����ֱ��AC��
��Q��AC��ʱ��������ã�BP=x��CQ=2x��PC=4-x��
��AB=BC=CA=4��
���C=60�㣻
��PQ��AC�����С�QPC=30�㣬
��PC=2CQ��
��4-x=2��2x��
��x=
��
��x=
��Q��AC�ϣ�ʱ��PQ��AC��
��ͼ����
��PQ��ABʱ��BP=x��BQ=
x��AC+AQ=2x��
��AC=4��
��AQ=2x-4��
��2x-4+
x=4��
��x=
��
��x=
ʱPQ��AB��
������������PQ��ABʱ��x=
��
��
��2��y=-
x2+
x��
��ͼ�ڣ���0��x��2ʱ��P��BD�ϣ�Q��AC�ϣ�����Q��QN��BC��N��
�ߡ�C=60�㣬QC=2x��
��QN=QC��sin60��=
x��
��AB=AC��AD��BC��
��BD=CD=
BC=2��
��DP=2-x��
��y=
PD•QN=
��2-x��•
x=-
x2+
x��
��3����0��x��2ʱ����Rt��QNC�У�QC=2x����C=60�㣻
��NC=x��
��BP=NC��
��BD=CD��
��DP=DN��
��AD��BC��QN��BC��
��AD��QN��
��OP=OQ��
��S��PDO=S��DQO��
��ADƽ�֡�PQD�������
��4����Ȼ��������x��ֵ��ʹ����PQΪֱ����Բ��AC���룬
��x=
��
ʱ����PQΪֱ����Բ��AC���У�
��0��x��
��
��x��
��
��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
 �⣺��1��
�⣺��1��| 4 |
| 5 |
| 16 |
| 5 |
��Q��AB��ʱ����ȻPQ����ֱ��AC��
��Q��AC��ʱ��������ã�BP=x��CQ=2x��PC=4-x��
��AB=BC=CA=4��
���C=60�㣻
��PQ��AC�����С�QPC=30�㣬
��PC=2CQ��
��4-x=2��2x��
��x=
| 4 |
| 5 |
��x=
| 4 |
| 5 |
��ͼ����
��PQ��ABʱ��BP=x��BQ=
| 1 |
| 2 |
��AC=4��
��AQ=2x-4��
��2x-4+
| 1 |
| 2 |
��x=
| 16 |
| 5 |
��x=
| 16 |
| 5 |
������������PQ��ABʱ��x=
| 4 |
| 5 |
| 16 |
| 5 |
��2��y=-
| ||
| 2 |
| 3 |
��ͼ�ڣ���0��x��2ʱ��P��BD�ϣ�Q��AC�ϣ�����Q��QN��BC��N��
�ߡ�C=60�㣬QC=2x��
��QN=QC��sin60��=
| 3 |
��AB=AC��AD��BC��
��BD=CD=
| 1 |
| 2 |
��DP=2-x��
��y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
��3����0��x��2ʱ����Rt��QNC�У�QC=2x����C=60�㣻
��NC=x��
��BP=NC��
��BD=CD��
��DP=DN��
��AD��BC��QN��BC��
��AD��QN��
��OP=OQ��
��S��PDO=S��DQO��
��ADƽ�֡�PQD�������
��4����Ȼ��������x��ֵ��ʹ����PQΪֱ����Բ��AC���룬
��x=
| 4 |
| 5 |
| 16 |
| 5 |
��0��x��
| 4 |
| 5 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 5 |
�����������ۺ������˵ȱ������ε����ʡ�ֱ�������ε������Լ�ֱ�ߺ�Բ��λ�ù�ϵ��⣮

��ϰ��ϵ�д�
 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
�����Ŀ
 20����ͼ���ڡ�ABC�У���BAC=45�㣬�ֽ���ABC�Ƶ�A��ʱ����ת30������ADE��λ�ã�ʹAC��DE�����B=
20����ͼ���ڡ�ABC�У���BAC=45�㣬�ֽ���ABC�Ƶ�A��ʱ����ת30������ADE��λ�ã�ʹAC��DE�����B= ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=1��ȡб�ߵ��е㣬��б�������ߣ�����һ���µĵ��������Σ���˼�����ȥ��ֱ����������ֱ�������ε�б�����ABC��BC�ص�����ʱ��������ε�б��Ϊ
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=1��ȡб�ߵ��е㣬��б�������ߣ�����һ���µĵ��������Σ���˼�����ȥ��ֱ����������ֱ�������ε�б�����ABC��BC�ص�����ʱ��������ε�б��Ϊ 2����ͼ���ڡ�ABC�У�DE��BC����ôͼ�����1��ȵĽ��ǣ�������
2����ͼ���ڡ�ABC�У�DE��BC����ôͼ�����1��ȵĽ��ǣ������� ��ͼ���ڡ�ABC�У�AB=AC���ҡ�A=100�㣬��B=
��ͼ���ڡ�ABC�У�AB=AC���ҡ�A=100�㣬��B=