题目内容
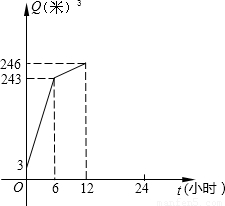
某工厂有一水塔装有两个相同的进水管与一个出水管(每小时每个进水管的进水量与出水管的出水量保持不变).工厂根据实际情况安装了自动控制系统来控制进水管与出水管开放的时间.设置的程序为:每天0点至6点,同时打开两个进水管;6点至12点,关闭一个进水管同时打开出水管;12点至24点,关闭另一个进 水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.
水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.(1)根据函数的图象回答从0点至12点,水塔中每小时增加的水量是多少米3?
(2)请你求出当12≤t≤24时,Q与t之间的函数的函数关系式,并画出函数的图象;
(3)请你利用所学过的数学知识,回答:从第一天0点起,第几天何时水塔中的储水量首次达到425米3?
分析:(1)根据图形即可得出水塔中每小时增加的水量以及出水量,即可得出水塔中每小时增加的水量;
(2)根据(1)中进出水管的出水与进水数据得出图形上点的坐标,即可得出解析式;
(3)根据已知得出每天水塔中净增水量,再依此求解.
(2)根据(1)中进出水管的出水与进水数据得出图形上点的坐标,即可得出解析式;
(3)根据已知得出每天水塔中净增水量,再依此求解.
解答:解:(1)根据函数的图象回答从0点至6点,水塔中每小时增加的水量是(243-3)÷6=40米3;
根据函数的图象回答从6点至12点,水塔中每小时增加的水量是(246-243)÷6=0.5米3.
水塔中每小时增加的水量是40米3和0.5米3;
(2)当12≤t≤24时,A点坐标为(12,246),
B点坐标纵为246-12×19.5=12,
∴B点坐标为:(24,12),
∴假设Q=kt+b,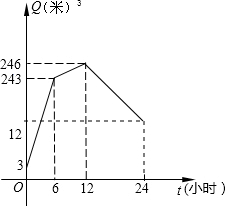
∴
,
解得:
,
∴Q=-19.5t+480;
(3)由(2)知,每天水塔中净增9m3,
当两进水管同时开放时,6小时进水240m3,
∴425-246=179,
∴182÷9≈20天,
∴从第一天0点起,第20天时水塔中的储水量首次达到425米3.
根据函数的图象回答从6点至12点,水塔中每小时增加的水量是(246-243)÷6=0.5米3.
水塔中每小时增加的水量是40米3和0.5米3;
(2)当12≤t≤24时,A点坐标为(12,246),
B点坐标纵为246-12×19.5=12,
∴B点坐标为:(24,12),
∴假设Q=kt+b,

∴
|
解得:
|
∴Q=-19.5t+480;
(3)由(2)知,每天水塔中净增9m3,
当两进水管同时开放时,6小时进水240m3,
∴425-246=179,
∴182÷9≈20天,
∴从第一天0点起,第20天时水塔中的储水量首次达到425米3.
点评:此题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质,注意数形结合的运用.

练习册系列答案
相关题目
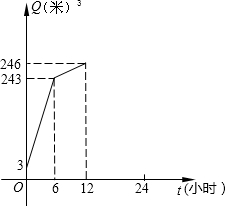 水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.
水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.