题目内容
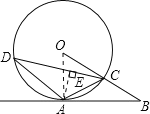
【题目】已知：如图，
是
上一点，半径
的延长线与过点的直线交于
点，
，
．
（1）求证：
是的切线；
（2）若
，
，求弦
的长．
【答案】（1）证明见解析（2）
【解析】
试题（1）求证：AB是
的切线，可以转化为证
的问题来解决．本题应先说明
是等边三角形，则
；又
进而可以得到
则可知
，即可求出
（2）作
于点
，
因而就可以转化为求
的问题，根据勾股定理就可以得到．
试题解析：(1)证明：如图，连接OA；
∴OC=BC=AC=OA.
∴△ACO是等边三角形.
∵AC=BC，
∴∠CAB=∠B，
又∠OCA为△ACB的外角，
∴∠OCA=∠CAB+∠B=2∠B，
∴
又
∴AB是的切线；
(2)作AE⊥CD于点E，
∵
∴
∵
∴在Rt△ACE中,
∵
∴
∴
∴
练习册系列答案
相关题目
