题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求此抛物线的解析式;
(2)设抛物线的顶点为![]() ,将直线
,将直线![]() 沿
沿![]() 轴向下平移两个单位得到直线
轴向下平移两个单位得到直线![]() ,直线
,直线![]() 与抛物线的对称轴交于
与抛物线的对称轴交于![]() 点,
点,![]() 求直线
求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,求到直线![]() 距离相等的点的坐标.
距离相等的点的坐标.
【答案】(1)y=![]() (2)y=
(2)y=![]() x(3)M(
x(3)M(![]() ,0)、A(0,2)、(0,-2)、(
,0)、A(0,2)、(0,-2)、(![]() ,0)
,0)
【解析】
试题(1)把![]() 坐标代入抛物线解析式即可.
坐标代入抛物线解析式即可.
(2)先设出平移后的直线![]() 的解析式,然后根据(1)的抛物线的解析式求出
的解析式,然后根据(1)的抛物线的解析式求出![]() 点的坐标,然后将
点的坐标,然后将![]() 点的坐标代入直线
点的坐标代入直线![]() 中即可得出直线
中即可得出直线![]() 的解析式.
的解析式.
(3)本题关键是找出所求点的位置,根据此点到直线![]() 的距离都相等,因此这类点应该有4个,均在
的距离都相等,因此这类点应该有4个,均在![]() 的内角平分线上(
的内角平分线上(![]() 外有3个,三条角平分线的交点是一个),可据此来求此点的坐标.
外有3个,三条角平分线的交点是一个),可据此来求此点的坐标.
试题解析:(1)根据题意得![]()
解得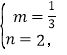
所以抛物线的解析式为:![]()
(2)由![]() 得抛物线的顶点坐标为
得抛物线的顶点坐标为![]()
依题意,可得![]() 且直线过原点,
且直线过原点,
设直线的解析式为y=kx,则![]()
解得![]()
所以直线l的解析式为![]()
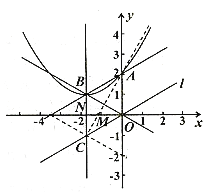
(3)到直线OB、OC、BC距离相等的点有四个,如图,
由勾股定理得OB=OC=BC=2,所以△OBC为等边三角形.
易证x轴所在的直线平分∠BOC,y轴是△OBC的一个外角的平分线,
作∠BCO的平分线,交x轴于![]() 点,交y轴于
点,交y轴于![]() 点,
点,
作△OBC的∠BCO相邻外角的角平分线,交y轴于![]() 点,
点,
反向延长线交x轴于![]() 点,可得点
点,可得点![]() 就是到直线OB、OC、BC距离相等的点.
就是到直线OB、OC、BC距离相等的点.
可证![]() 均为等边三角形,可求得:
均为等边三角形,可求得:
①![]() 所以点
所以点![]() 的坐标为
的坐标为![]()
②点![]() 与点A重合,所以点
与点A重合,所以点![]() 的坐标为(0,2),
的坐标为(0,2),
③点 ![]() 与点A关于x轴对称,所以点
与点A关于x轴对称,所以点![]() 的坐标为(0,2),
的坐标为(0,2),
④设抛物线的对称轴与x轴的交点为N,
![]() 且
且![]()
所以点![]() 的坐标为
的坐标为![]()
综合所述,到直线OB、OC、BC距离相等的点的坐标分别为:
![]()

练习册系列答案
相关题目








