��Ŀ����
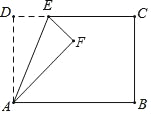
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�P��BC����һ���㣨����B��C�����غϣ�������ABP��ֱ��AP���ۣ���B���ڵ�E������CD��ȡһ��M��ʹ�ý���CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������AM��AN��

��1����PΪBC���е㣬��sin��CPM=________��
��2����֤����PAN�Ķ������䣻
��3����P��BC�����˶�ʱ����ADM������Ƿ������Сֵ�������ڣ������PB�ij����������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��֤������������3��������Сֵ��BP��2.
����2��֤������������3��������Сֵ��BP��2.
�������������������1�����������ε����ʺ��ɶ������AP���������ҵĶ���õ�sin��BAP��![]() �������۵�������֤����CPM����BAP���õ��𰸣�
�������۵�������֤����CPM����BAP���õ��𰸣�
��2��֤��Rt��AEN��Rt��ADN���õ���EAN����DAN�����㼴�ɣ�
��3����PB��x���������������ε��������DM�����������ε������ʽ�õ����κ����Ľ���ʽ��Ȼ����ʽת��Ϊ����ʽ�����ɵó�����
���������
�⣺��1����������ABCD�ı߳�Ϊ4��PΪBC���е㣬
��BP��![]() PC��2��
PC��2��
��AP��![]() ��2
��2![]() ��
��
��sin��BAP��![]() ��
��
���۵������ʿ�֪����BPA����EPA����CPM����FPM��
���APM��![]() ����BPE����CPF����90����
����BPE����CPF����90����
���BPA����CPM��90�����֡�BPA����BAP��90����
���CPM����BAP��
��sin��CPM��sin��BAP��![]() ��
��
�ʴ�Ϊ�� ![]() ��
��
��2���⣺���۵������ʿ�֪����AEP����B��90����AE��AB����BAP����EAP��
��AE��AD��
��Rt��AEN��Rt��ADN��
AE��AD��AN��AN��
��Rt��AEN��Rt��ADN��
���EAN����DAN��
���PAN��![]() ��BAD��45����
��BAD��45����
��3���⣺��PB��x����PC��4��x��
�ߡ�CPM����BAP����ABP����PCM��90����
���ABP�ס�PCM��
��![]() ����
����![]() ��
��
��ã�CM����![]() x2��x��
x2��x��
��DM��4������![]() x2��x����
x2��x���� ![]() x2��x��4��
x2��x��4��
���ADM�������![]() ��4����
��4����![]() x2��x��4����
x2��x��4����![]() ��x��2��2��6��
��x��2��2��6��
�൱BP��2ʱ����ADM�����������Сֵ6��