题目内容
【题目】如图,将平行四边形ABCD的对角线BD向两个方向延长至点E和点F,使BE=DF,求证:四边形AECF是平行四边形. 
【答案】证明:连接A、C,设AC与BD交于点O. ∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
又∵BE=DF,∴OE=OF.
∴四边形AECF是平行四边形.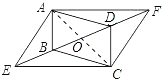
【解析】要证四边形AECF是平行四边形,结合图形知BF是其一条对角线,故需连接另一条对角线AC,由四边形ABCD是平行四边形易知OA=OC,OC=OD,只要再证得OE=OF即可.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
相关题目