题目内容
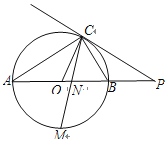
【题目】如图,正方形![]() 中,点
中,点![]() 是边
是边![]() 上异于点
上异于点![]() 的一点,
的一点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于
于![]() ,连
,连![]() .
.
(1)求证:![]() ;
;
(2)请求出:![]() 的度数;
的度数;
(3)试猜想线段![]() 之间的数量关系并说明理由.
之间的数量关系并说明理由.

【答案】(1)证明见解析 (2)90° (3)AE=DF+BM
【解析】
(1)本题考查垂直平分线的性质,按照其性质直接作答即可.
(2)本题考查全等三角形的判定,可通过做辅助线构造全等三角形,继而通过角度的等量替换解答本题.
(3)本题考查线段之间的数量关系,需要通过做辅助线构造全等三角形,利用全等性质推出边等,最后进行边的替换解答本题.
(1)∵EF是AM的垂直平分线
又∵点K在线段EF上
∴ KA=KM
(2)过K点作KQ,KT分别垂直于AB,BC,如下图所示
∵正方形ABCD,点K在其对角线BD上
∴KQ=KT,四边形QKTB为正方形
又∵KA=KM,∠KQA=∠KTM=90°
∴△KAQ![]() △KMT(HL)
△KMT(HL)
∴∠AKQ=∠TKM
∵∠QKT=90°
∴∠QKT=∠QKM+∠MKT=90°
∴∠QKT=∠QKM+∠AKQ=90°
∴∠AKM=90°

(3)过F点作FG⊥AB于G点,如下图所示
∴AG=DF,∠FEG+∠GFE=90°
∵EF⊥AM
∴∠BAM+∠FEG=90°
∴∠BAM=∠GFE
又∵∠FGE=∠ABM=90°,GF=AB
∴△FGE![]() △ABM(ASA)
△ABM(ASA)
∴GE=BM
故AE=AG+GE=DF+BM


练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目