题目内容
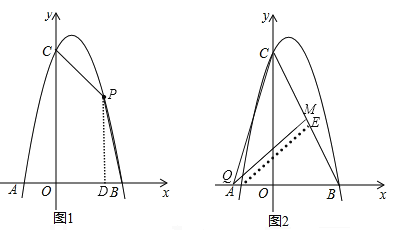
【题目】如图1，对称轴为直线x=
的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A．
（1）求抛物线的解析式；
（2）若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；
（3）如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】（1）
；（2）6；（3）Q（
，0）．
【解析】
试题分析：（1）由对称轴的对称性得出点A的坐标，由待定系数法求出抛物线的解析式；
（2）作辅助线把四边形COBP分成梯形和直角三角形，表示出面积S，化简后是一个关于S的二次函数，求最值即可；
（3）画出符合条件的Q点，只有一种，①利用平行相似得对应高的比和对应边的比相等列比例式；②在直角△OCQ和直角△CQM利用勾股定理列方程；两方程式组成方程组求解并取舍．
试题解析：（1）由对称性得：A（﹣1，0），设抛物线的解析式为：y=a（x+1）（x﹣2），把C（0，4）代入：4=﹣2a，a=﹣2，∴y=﹣2（x+1）（x﹣2），∴抛物线的解析式为：；
（2）如图1，设点P（m，
），过P作PD⊥x轴，垂足为D，∴S=S梯形+S△PDB=
，∴S=
=
，∵﹣2＜0，∴S有最大值，则S大=6；
（3）如图2，存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形，理由是：
设直线BC的解析式为：y=kx+b，把B（2，0）、C（0，4）代入得：
，解得：
，∴直线BC的解析式为：y=﹣2x+4，设M（a，﹣2a+4），过A作AE⊥BC，垂足为E，则AE的解析式为：
，则直线BC与直线AE的交点E（1.4，1.2），设Q（﹣x，0）（x＞0），∵AE∥QM，∴△ABE∽△QBM，∴
①，由勾股定理得：
②，由①②得：
=4（舍），
=
，当a=
时，x=
，∴Q（，0）．
