��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x����y���ϣ���֪OA=6��OB=10����DΪy����һ�㣬������Ϊ(0��2)����P�ӵ�A������ÿ��2����λ���ٶ����߶�AC��CB�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮
(1)����P������Cʱ����ֱ��DP�ĺ�������ʽ��
(2)��ͼ�ڣ��ѳ���������OP�۵�����B�Ķ�Ӧ��B��ǡ������AC���ϣ����P�����꣮
(3)��P���˶��������Ƿ����ʹ��BDPΪ���������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1) y=![]() x+2��(2)��������(3)���ڣ����������P����Ϊ(6�� 6)��(6��
x+2��(2)��������(3)���ڣ����������P����Ϊ(6�� 6)��(6�� ![]() )��(6��
)��(6��![]() )��
)��
��������
��1����ֱ��DP����ʽΪy=kx+b����D��B����������k��b��ֵ������ȷ��������ʽ����2���ٵ�P��AC��ʱ��������ODP��OD���Ϊ�̶�ֵ�������ʱ�������P��BC��ʱ���ױ�ODΪ�̶�ֵ����ʾ���ߣ������г�S��t�Ĺ�ϵʽ���ڵ���B�Ķ�Ӧ��B��ǡ������AC����ʱ���ؼ����ɶ������������ʱP���ꣻ��3�����ڣ��ֱ���BD��DP��BPΪ�ױ�����������ǣ����ù��ɶ�����ͼ���������������P���꼴�ɣ�
(1)��OA=6��OB=10���ı��� OACB Ϊ�����Σ���C(6��10)�� ���ʱֱ�� DP ����ʽΪ y=kx+b��
��(0��2)��C(6��10)�ֱ���룬��![]() �����
�����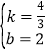 ��
��
���ʱֱ�� DP ����ʽΪ y=![]() x+2��
x+2��

(2)�ٵ��� P ���߶� AC ��ʱ��OD=2����Ϊ 6��S=6�� ���� P ���߶� BC ��ʱ��OD=2����Ϊ 6+10��2t=16��2t��S= 1 ��2��(16��2t)=��2t+16��
���� P(m,10������PB=![]() =m����ͼ 2�� ��
=m����ͼ 2�� ��![]() =OB=10�� OA=6��
=OB=10�� OA=6��

��![]() ��
��![]() =10��8=2��
=10��8=2��
��PC=6��m����m2=22+(6��m)2�����m=![]() �����ʱ��P��������(
�����ʱ��P��������(![]() ��10)��
��10)��
(3)���ڣ�����Ϊ������BDPΪ���������Σ�������������ǣ���ͼ3��
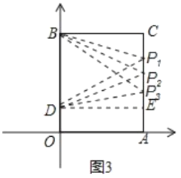
��BD=BPl=OB��OD=10��2=8���� Rt��BCP1 ��BP1=8�� BC=6��
���ݹ��ɶ����ã�![]() ����P1(6��
����P1(6��![]() )��
)��
�ڵ�BP2= DP2ʱ����ʱP2(6��6)��
�۵�DB=DP3=8ʱ����Rt��DEP3�У�DE=6�����ݹ��ɶ����ã�
![]() ����
����![]() ����P3 (6��
����P3 (6��![]() )��
)��
���ϣ����������P����Ϊ(6�� 6)��(6�� ![]() )��(6��
)��(6��![]() )��
)��




