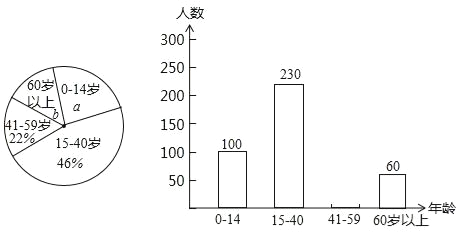
题目内容
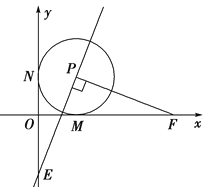
【题目】已知O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N.点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连结PF,过点P作PE⊥PF交y轴于点E.设点F运动的时间是t秒(t>0).
(1)求点E的坐标(用t表示);
(2)在点F运动过程中,当PF=2OE时,求t的值.
(3)当t>1时,作点F关于点M的对称点F′.点Q是线段MF′的中点,连结QE.在点F运动过程中,是否存在某一时刻,使得△QOE与△PMF相似,若存在,求出t的值;若不存在,请说明理由.
【答案】(1)E(0,1-t);(2)![]() 或
或![]() ;(3)存在:当t=
;(3)存在:当t=![]() ,t=
,t=![]() ,t=2+
,t=2+![]() 时,使得△QOE与△PMF相似.
时,使得△QOE与△PMF相似.
【解析】试题分析:
(1)连接PM、PN,由已知条件易证△PMF≌△PNE,由此可得NE=MF=t,则可得OE=t-1,结合点E在y轴的负半轴即可得到点E的坐标了;
(2)在Rt△PFM中,易得PF=![]() ,结合OE=
,结合OE=![]() 即可得到方程
即可得到方程![]() ,解此方程即可求得对应的t的值;
,解此方程即可求得对应的t的值;
(3)由F(1+t,0),F和F′关于点M对称可得F′(1-t,0),结合点Q是线段MF′的中点可得Q(1-![]() t,0),然后在1<t<2时,分△OEQ∽△MPF和△OEQ∽△MFP两种情况讨论计算可求得对应的t的值;在当t>2时,分△OEQ ∽△MPF和△OEQ ∽△MFP两种情况讨论计算可求得对应的t的值.
t,0),然后在1<t<2时,分△OEQ∽△MPF和△OEQ∽△MFP两种情况讨论计算可求得对应的t的值;在当t>2时,分△OEQ ∽△MPF和△OEQ ∽△MFP两种情况讨论计算可求得对应的t的值.
试题解析:
(1)如下图,连结PM,PN.
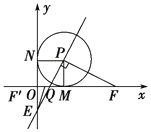
∵以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N,
∴∠PNE=∠PMF=∠MPN=90°,
∴∠NPE+∠EPM=∠EPM+∠MPF=90°,
∴∠NPE=∠MPF,
又∵PM=PN,
∴△PMF≌△PNE,
∴NE=MF=t,
∴OE=t-1,
∴E(0,1-t);
(2)在直角△PMF中![]() ,
, ![]() ,
,
由PF=2OE得![]()
![]() ,
,
解得![]() 或
或![]() .
.
(3)存在,理由如下;
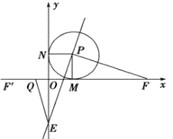
∵F(1+t,0),F和F′关于点M对称,
∴F′(1-t,0),
∵点Q是MF′的中点,
∴Q(1-![]() t,0),
t,0),
①当1<t<2时,如图,有OQ=1-![]() t,
t,
由(1)得∴NE=MF=t,OE=t-1.
当△OEQ∽△MPF时,
∴![]() ,
,
∴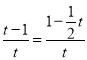 ,
,
解得,t=![]() 或t=
或t=![]() (舍去);
(舍去);
当△OEQ∽△MFP时, ![]() ,
,
∴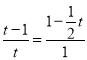 ,解得,t=
,解得,t=![]() 或t=
或t=![]() (舍去);
(舍去);
②当t>2时,如图,有OQ=![]() t-1,
t-1,
由(1)得NE=MF=t,OE=t-1,
当△OEQ ∽△MPF, ![]() ,
,
∴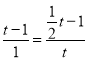 ,无解;
,无解;
当△OEQ ∽△MFP时, ![]() ;
;
∴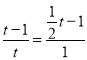 ,
,
解得![]() 或
或![]() (舍去).
(舍去).
综上所述,当t=![]() ,t=
,t=![]() ,
, ![]() 时,使得△QOE与△PMF相似.
时,使得△QOE与△PMF相似.

 阅读快车系列答案
阅读快车系列答案