题目内容
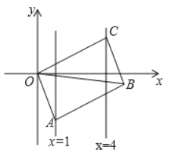
【题目】如图, ![]() 是
是 ![]() 内一点,
内一点, ![]() 与
与 ![]() 相交于
相交于 ![]() 、
、![]() 两点,且与
两点,且与 ![]() 、
、![]() 分别相切于点
分别相切于点 ![]() 、
、![]() ,
, ![]() .连接
.连接 ![]() 、
、![]() .
.
(1)求证: ![]() .
.
(2)已知 ![]() ,
, ![]() .求四边形
.求四边形 ![]() 是矩形时
是矩形时 ![]() 的半径.
的半径.

【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由AB、AC和⊙O相切于点D、E可得AD=AE,由此可得∠ADE=∠AED,结合DE∥BC,可得∠B=∠C,即可得到AB=AC了;
(2)如下图,连接AO交DE于点M,延长AO交BC于点N,连接OD、OE和DG,设⊙O的半径为r,由已知条件易证BN=3,∠ANB=90°,从而可得AN=4,在证△ADO∽△ANB,由此可得![]() ,即
,即![]() 从而可得AD=
从而可得AD= ![]() ,则BD=
,则BD= ![]() ,再证△BDG∽△BNA可得
,再证△BDG∽△BNA可得![]() ,即
,即 ,由此即可解得:
,由此即可解得: ![]() .
.
试题解析:
(1)∵![]() 与
与 ![]() 、
、![]() 分别相切于点
分别相切于点 ![]() 、
、![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() ;
;
(2) 如图,连接 ![]() ,交
,交 于点
![]() ,延长
,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,连接OD、
,连接OD、 ![]() 、
、![]() ,设
,设 ![]() 的半径为
的半径为 ![]() ,
,
∵ 四边形 ![]() 是矩形,
是矩形,
∴∠DEG=90°,
∴![]() 是
是 ![]() 的直径.
的直径.
∵![]() ,AN平分∠BAC,
,AN平分∠BAC,
∴![]() ∠ANB=90°,
∠ANB=90°,
∴在Rt△ABN中可得:AN=4,
∵AB和⊙O相切于点D,
∴∠ADO=∠GDB=90°=∠ANB,
∵∠DAO=∠NAB,
∴△ADO∽△ANB,
∴![]() ,即
,即![]() ,
,
∴AD= ![]() ,
,
∵∠GDB=∠ANB=90°,∠B=∠B,
∴△BDG∽△BNA,
∴![]() ,即
,即 ,解得:
,解得: ![]() .
.
∴四边形 ![]() 是矩形时
是矩形时 ![]() 的半径为
的半径为 ![]() .
.


【题目】华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 25 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?