��Ŀ����
����Ŀ�����⣺��1����ͼ�٣���Rt��ABC�У�AB��AC��DΪBC����һ�㣨�����B��C�غϣ������߶�AD�Ƶ�A��ʱ����ת90��õ�AE������EC�����߶�BC��DC��EC֮������ĵ�����ϵʽΪ�� ����
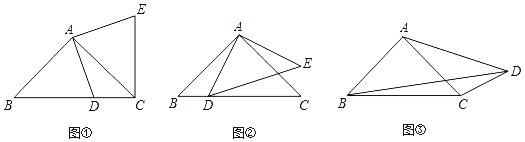
̽������2����ͼ�ڣ���Rt��ABC��Rt��ADE�У�AB��AC��AD��AE������ADE�Ƶ�A��ת��ʹ��D����BC���ϣ���̽���߶�AD��BD��CD֮������ĵ�����ϵ����֤����Ľ��ۣ�
Ӧ�ã���3����ͼ�ۣ����ı���ABCD�У���ABC����ACB����ADC��45�㣮��BD��9��CD��3����AD�ij���
���𰸡���1��BC��DC��EC����2��BD2��CD2��2AD2����3��AD��6.
��������
��1����֤��BAD�ա�CAE�����ɵõ�BC��DC��EC
��2������CE����֤��BAD�ա�CAE���ٵõ�ED��![]() AD��Ȼ����Rt��ECD�����ù��ɶ�������������ϵ��
AD��Ȼ����Rt��ECD�����ù��ɶ�������������ϵ��
��3�����߶�AD�Ƶ�A˳ʱ����ת90���õ�AE������CE��BE����֤��ABE�ա�ACD����������Rt��BED�У��ɹ��ɶ�������DE2��BD2��BE2����2AD2��BD2��CD2���ٽ��AD�ij�����.
�⣺(1)BC��DC��EC��
�ߡ�BAC����DAE��90����
���BAC����DAC����DAE����DAC������BAD����CAE.
�ڡ�BAD�͡�CAE�У�
���BAD�ա�CAE(SAS)��
��BD��CE��
��BC��BD��CD��EC��CD��
(2)BD2��CD2��2AD2.
֤�����£�
����CE�����ͼ1��ʾ��
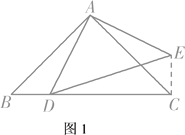
�ߡ�BAC����BAD����DAC��90����AB��AC��
���ABC����ACB��45��.
�ߡ�DAE����CAE����DAC��90����
���BAD����CAE.
�ڡ�BAD�͡�CAE�У�
���BAD�ա�CAE(SAS)��
��BD��CE����ACE����ABC��45����
���BCE����ACB����ACE��90��.
�ߡ�EAD��90����AE��AD��
��ED��![]() AD��
AD��
��Rt��ECD�У��ɹ��ɶ�����
��ED2��CE2��CD2��
��BD2��CD2��2AD2.
(3)���߶�AD�Ƶ�A˳ʱ����ת90���õ�AE������CE��BE��
���ͼ2��ʾ����AE��AD����EAD��90����
���EAD�ǵ���ֱ�������Σ�
��DE��![]() AD����AED��45��.
AD����AED��45��.
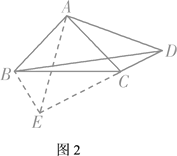
�ߡ�ABC����ACB��ADC��45����
���BAC��90����AB��AC��
ͬ(2)�ķ�������֤�á�ABE�ա�ACD��
��BE��CD����AEB����ADC��45����
���BEC����AEB����AED��90��.
��Rt��BED�У��ɹ��ɶ�������DE2��BD2��BE2��
��2AD2��BD2��CD2.
��BD��9��CD��3��
��2AD2��92��32��72��
��AD��6(��ֵ����ȥ)��

 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�