题目内容
如图1,抛物线y=ax2-2ax-b(a<0)与x轴的一个交点为B(-1,0),与y轴的正半轴交于点C,顶点为D.(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的解析式;
②如图2,点E是y轴负半轴上的一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
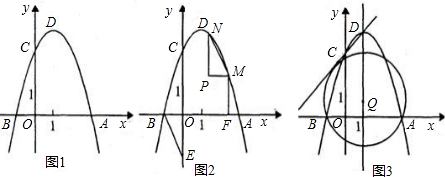
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
分析:(1)将B点坐标代入抛物线的解析式中,可得到a、b的关系式,将a替换b后,将抛物线的解析式化为顶点坐标式,即可得到顶点D的坐标.
(2)①根据(1)题所得抛物线解析式,可用得到C、A的坐标,若以AD为直径的圆经过点C,由圆周角定理可知∠ACD=90°,分别用a表示出AC、AD、CD的长,根据勾股定理可得到关于a的方程,即可求出a的值,进而确定该抛物线的解析式.
②根据①题抛物线的解析式,可求得点B的坐标,先设出点M的坐标,可用其横坐标表示出BF的长,已知BF=2MF,即可得到M点纵坐标的表达式,将其代入抛物线的解析式中,即可得到点M的坐标;根据中心对称图形的性质知MP=BO,由此可求得点P(即点N)的横坐标,将其代入抛物线的解析式中,即可得到点N的坐标.
③若⊙Q与直线CD相切(设切点为K),那么QK=QB=QA,可设出点Q的坐标(横坐标已知,只设纵坐标即可),可表示出QB、QK、DQ的长;设直线DC与x轴的交点为G,易求得直线DC的解析式,进而可得到点G的坐标,由此可求得HG、DG的长(H为抛物线对称轴与x轴交点),由于直线CD切⊙Q于点K,易证得△DQK∽△DGH,根据抛物线所得比例线段,即可得到关于点Q纵坐标的方程,通过解方程可确定点Q的坐标.
(2)①根据(1)题所得抛物线解析式,可用得到C、A的坐标,若以AD为直径的圆经过点C,由圆周角定理可知∠ACD=90°,分别用a表示出AC、AD、CD的长,根据勾股定理可得到关于a的方程,即可求出a的值,进而确定该抛物线的解析式.
②根据①题抛物线的解析式,可求得点B的坐标,先设出点M的坐标,可用其横坐标表示出BF的长,已知BF=2MF,即可得到M点纵坐标的表达式,将其代入抛物线的解析式中,即可得到点M的坐标;根据中心对称图形的性质知MP=BO,由此可求得点P(即点N)的横坐标,将其代入抛物线的解析式中,即可得到点N的坐标.
③若⊙Q与直线CD相切(设切点为K),那么QK=QB=QA,可设出点Q的坐标(横坐标已知,只设纵坐标即可),可表示出QB、QK、DQ的长;设直线DC与x轴的交点为G,易求得直线DC的解析式,进而可得到点G的坐标,由此可求得HG、DG的长(H为抛物线对称轴与x轴交点),由于直线CD切⊙Q于点K,易证得△DQK∽△DGH,根据抛物线所得比例线段,即可得到关于点Q纵坐标的方程,通过解方程可确定点Q的坐标.
解答: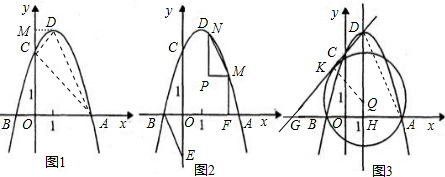 解:(1)把B(-1,0)代入得:b=3a,(1分)
解:(1)把B(-1,0)代入得:b=3a,(1分)
y=ax2-2ax-3a=a(x-1)2-4a,
所以顶点D(1,-4a).(2分)
(2)①有题设知:点C(0,-3a),点A(3,0),
且∠ACD=90°;(3分)
在Rt△AOC中,AC2=9a2+32,
在Rt△AHD中,AD2=16a2+22,
在Rt△CMD中,CD2=a2+12,
因为AD2=AC2+CD2,
所以16a2+22=a2+12+9a2+32,a2=1,又a<0,
所以a=-1,(4分)
抛物线的解析式为y=-x2+2x+3.
②设点M(m,y1)
则BF=m+1,
点MF:BF=1:2,
∴MF=
,即y1=
(5分)
点M(m,y1)在抛物线上,
所以
=-m2+2m+3,
解得:m=
或m=-1(舍去),
点M的坐标为M(
,
);(6分)
又因为MP∥BO,MP=BO,
所以点的坐标为P(
,
),
由
得点N的坐标为N(
,
).(7分)
③设点Q(1,y)
因为D(1,4),C(0,3)
直线CD的方程为y=x+3,(8分)
令y=0,得G(-3,0),
设直线CD与⊙O的切点为K,连接QK;
则△DQK∽△DGH,
=
,(9分)
又QK=QB=
,DQ=4-y,
所以
=
,
整理得:y2+8y-8=0,
解得y=-4±2
;
所以点Q的坐标为(1,-4+2
)或(1,-4-2
).(10分)
说明:由∠QDK=45°,直接得出QD=
QK,从而得4-y=
再求解,同样给分.
 解:(1)把B(-1,0)代入得:b=3a,(1分)
解:(1)把B(-1,0)代入得:b=3a,(1分)y=ax2-2ax-3a=a(x-1)2-4a,
所以顶点D(1,-4a).(2分)
(2)①有题设知:点C(0,-3a),点A(3,0),
且∠ACD=90°;(3分)
在Rt△AOC中,AC2=9a2+32,
在Rt△AHD中,AD2=16a2+22,
在Rt△CMD中,CD2=a2+12,
因为AD2=AC2+CD2,
所以16a2+22=a2+12+9a2+32,a2=1,又a<0,
所以a=-1,(4分)
抛物线的解析式为y=-x2+2x+3.
②设点M(m,y1)
则BF=m+1,
点MF:BF=1:2,
∴MF=
| m+1 |
| 2 |
| m+1 |
| 2 |
点M(m,y1)在抛物线上,
所以
| m+1 |
| 2 |
解得:m=
| 5 |
| 2 |
点M的坐标为M(
| 5 |
| 2 |
| 7 |
| 4 |
又因为MP∥BO,MP=BO,
所以点的坐标为P(
| 3 |
| 2 |
| 7 |
| 4 |
由
|
| 3 |
| 2 |
| 15 |
| 4 |
③设点Q(1,y)
因为D(1,4),C(0,3)
直线CD的方程为y=x+3,(8分)
令y=0,得G(-3,0),
设直线CD与⊙O的切点为K,连接QK;
则△DQK∽△DGH,
| DQ |
| DG |
| QK |
| GH |
又QK=QB=
| 4+y2 |
所以
| 4-y | ||
4
|
| ||
| 4 |
整理得:y2+8y-8=0,
解得y=-4±2
| 6 |
所以点Q的坐标为(1,-4+2
| 6 |
| 6 |
说明:由∠QDK=45°,直接得出QD=
| 2 |
| 2 |
| 4+y2 |
点评:此题考查了二次函数解析式的确定、圆周角定理、勾股定理、相似三角形的判定和性质以及中心对称图形的性质、直线与圆的位置关系等重要知识,涉及知识面广,难度较大.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
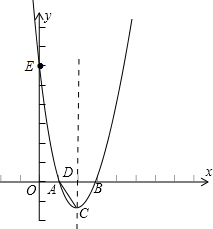 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=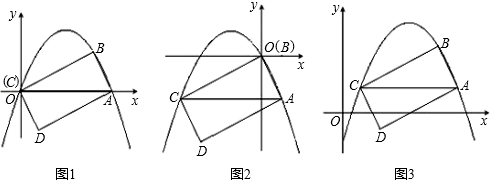
 如图,将抛物线
如图,将抛物线