题目内容
已知α、β是方程x2-7x+8=0的两根,且α>β,则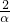 +3β2的值为
+3β2的值为
- A.
 (403+85
(403+85 )
) - B.
 (403-85
(403-85 )
) - C.95
- D.

A
分析:先设p=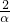 +3β2,q=
+3β2,q=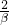 +3α2,再求出p+q及p-q的表达式,利用韦达定理求出其值p+q及p-q的值,根据α>β即可求出代数式的值.
+3α2,再求出p+q及p-q的表达式,利用韦达定理求出其值p+q及p-q的值,根据α>β即可求出代数式的值.
解答:设p=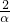 +3β2,q=
+3β2,q=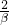 +3α2,
+3α2,
∴p+q=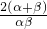 +3(α+β)2-6αβ
+3(α+β)2-6αβ
p-q=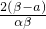 +3(α-β)(α+β)
+3(α-β)(α+β)
∵α、β是方程x2-7x+8=0的两根,
∴α+β=7,αβ=8,
∴(α-β)2=(α+β)2-4αβ=17,
∵α>β,则α-β= ,代入后得p+q=
,代入后得p+q=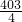 ,p-q=
,p-q=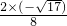 +3×
+3× ×7=
×7=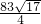 ,
,
∴p= (403+83
(403+83 )即则
)即则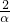 +3β2=
+3β2= (403+83
(403+83 ).
).
故选A.
点评:本题考查的是一元二次方程根与系数的关系及代数式求值,根据题意设出p=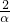 +3β2,q=
+3β2,q=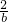 +3α2,是解答此题的关键.
+3α2,是解答此题的关键.
分析:先设p=
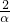 +3β2,q=
+3β2,q=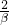 +3α2,再求出p+q及p-q的表达式,利用韦达定理求出其值p+q及p-q的值,根据α>β即可求出代数式的值.
+3α2,再求出p+q及p-q的表达式,利用韦达定理求出其值p+q及p-q的值,根据α>β即可求出代数式的值.解答:设p=
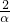 +3β2,q=
+3β2,q=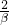 +3α2,
+3α2,∴p+q=
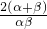 +3(α+β)2-6αβ
+3(α+β)2-6αβp-q=
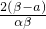 +3(α-β)(α+β)
+3(α-β)(α+β)∵α、β是方程x2-7x+8=0的两根,
∴α+β=7,αβ=8,
∴(α-β)2=(α+β)2-4αβ=17,
∵α>β,则α-β=
 ,代入后得p+q=
,代入后得p+q=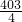 ,p-q=
,p-q=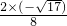 +3×
+3× ×7=
×7=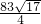 ,
,∴p=
 (403+83
(403+83 )即则
)即则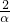 +3β2=
+3β2= (403+83
(403+83 ).
).故选A.
点评:本题考查的是一元二次方程根与系数的关系及代数式求值,根据题意设出p=
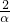 +3β2,q=
+3β2,q=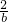 +3α2,是解答此题的关键.
+3α2,是解答此题的关键. 
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
已知a,b是方程x2-2x-1=0的两个根,则a2+a+3b的值是( )
| A、7 | ||
| B、-5 | ||
C、7
| ||
| D、-2 |