题目内容
阅读下面材料：设一元二次方程ax2+bx+c=0的两根为x1、x2，则两根与方程中各系数之间有如下关系：x1+x2=-
| b |
| a |
| c |
| a |
根据该材料解答下列问题：已知a、b是方程x2+6x-3=0的两个实数根；
（1）则a+b=
（2）求
| a |
| b |
| b |
| a |
分析：（1）利用根与系数的关系可求出a+b，ab的值；
（2）先把
+
通分，然后把a+b，ab的值整体代入即可求值．
（2）先把
| a |
| b |
| b |
| a |
解答：解：（1）a+b=-
=-6，a•b=
=-3，
（2）
+
=
=
=
=-14．
| 6 |
| 1 |
| -3 |
| 1 |
（2）
| a |
| b |
| b |
| a |
| a2+b2 |
| ab |
| (a+b)2-2ab |
| ab |
| (-6)2-2×(-3) |
| -3 |
点评：一元二次方程的两个根x1、x2具有这样的关系：x1+x2=-
，x1•x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
相关题目
，
；
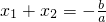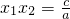的值．
，x1x2=
．∵
，∴
=a[x2-（x1+x2）x+x1x2]=a（x-x1）（x-x2）．于是，二次三项式就可以分解因式ax2+bx+c=a（x-x1）（x-x2）．
，
；
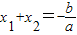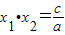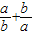的值．