��Ŀ����
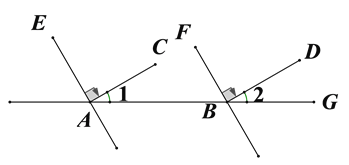
����Ŀ��(12��)��֪����ƽ��ֱ������ϵ��,AB��x���ڵ�B,��A(a,b)����![]() +|b-2|=0,ƽ���߶�ABʹ��A��ԭ���غ�,��B�Ķ�Ӧ��Ϊ��C.
+|b-2|=0,ƽ���߶�ABʹ��A��ԭ���غ�,��B�Ķ�Ӧ��Ϊ��C.
(1)��a=____,b=____;��C����Ϊ________;
(2)����ͼ��ʾ����D(m, n)���߶�BC��,��m��n����Ĺ�ϵʽ;

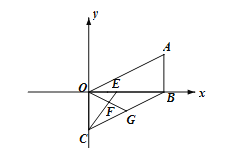
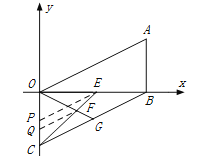
(3)����ͼ��ʾ��E���߶�OB��һ����,��OBΪ������G=��AOB,,��BC�ڵ�G����CE��OG�ڵ�F,�ĵ���E���߶�OB���˶�������, ![]() ��ֵ�Ƿ�ᷢ���仯?���仯��˵������,������,�������ֵ.
��ֵ�Ƿ�ᷢ���仯?���仯��˵������,������,�������ֵ.
���𰸡� ��1��4 2 ��0����2������2��m-2n=4;(3)���䣬 ![]() ���ɼ�����.
���ɼ�����.
����������1��a= 4 ��b= 2 ����C��������0��-2����
��2����ͼ1������D�ֱ���DM��x���ڵ�M�� DN��y���ڵ�N������OD��
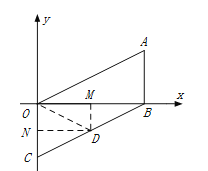
��AB�� x���ڵ�B���ҵ�A��D��C���������ֱ�Ϊ����4��2������m��n������0��-2��
��OB=4��OC=2��MD=-n��ND=m
�� S��BOC=![]()
![]() OB��OC=4
OB��OC=4
�֡�S��BOC = S��BOD��S��COD
=![]() OB��MD��
OB��MD��![]() OC��ND
OC��ND
=![]() ��4����-n��+
��4����-n��+![]() ��m��2
��m��2
=m-2n
��m-2n=4��������(7��)
��3���⣺ ![]()
![]() ��ֵ���䣬ֵΪ2���������£�
��ֵ���䣬ֵΪ2���������£�
��ͼ��ʾ���ֱ����E��F��EP��OA�� FQ��OA�ֱ�y���ڵ�P����Q
���߶�OC�����߶�ABƽ�Ƶõ�
��BC��OA �֡�EP��OA
��EP��BC
���GCF=��PEC
��EP��OA
���AOE=��OEP
���OEC=��OEP+��PEC
=��AOE+��GCF ͬ������OFC=��AOF+��GCF��������(10��)
�֡ߡ�AOB=��BOG
���OFC=2��AOE+��GCF
��![]()
![]()
![]() =2
=2