Question

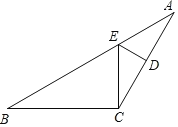
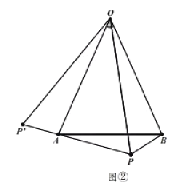
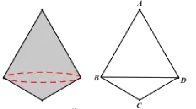
【题目】如图，某物体由上下两个圆锥组成，其轴截面中，，.若下部圆锥的侧面积为1，则上部圆锥的侧面积为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

先证明△ABD为等边三角形，得到AB=AD=BD，∠A=∠ABD=∠ADB=60°，由求出∠CBD=∠CDB=30°，从而求出BC和BD的比值，利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，从而得到上部圆锥的侧面积．

解：∵∠A=60°，AB=AD，
∴△ABD为等边三角形，
∴AB=AD=BD，∠A=∠ABD=∠ADB=60°，

∵∠ABC=90°，
∴∠CBD=30°，

而CB=CD，
∴△CBD为底角为30°的等腰三角形，

过点C作CE⊥BD于点E，

易得BD=2BE，

∵∠CBD=30°，

∴BE：BC=：2，

∴BD：BC=：2=：1，即AB：BC=：1，

∵上面圆锥与下面圆锥的底面相同，
∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，
∴下面圆锥的侧面积=．
故选：C．