题目内容
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 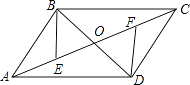
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中 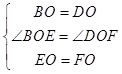 ,
,
∴△BOE≌△DOF(SAS)
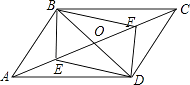
(2)证明:四边形EBDF为菱形,
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBDF为菱形.
【解析】(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.

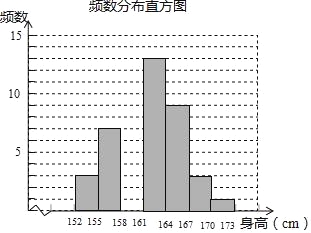
【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
身高分组 | 频数 | 频率 |
152≤x<155 | 3 | 0.06 |
155≤x<158 | 7 | 0.14 |
158≤x<161 | m | 0.28 |
161≤x<164 | 13 | n |
164≤x<167 | 9 | 0.18 |
167≤x<170 | 3 | 0.06 |
170≤x<173 | 1 | 0.02 |
根据以上统计图表完成下列问题:
(1)统计表中m= ,n= ,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在: 范围内;
(3)在身高≥167cm的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
【题目】老师想知道某校学生每天上学路上要花多少时间,于是随机选取30名同学每天来校的大致时间(单位:分钟)进行统计,统计表如下:
时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
(1)写出这组数据的中位数和众数;
(2)求这30名同学每天上学的平均时间.