题目内容
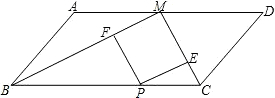 如图,点M是平行四边形ABCD的边AD的中点,点P是边BC上的一个动点,PE∥MB,PF∥MC,分别交MC于点E、交MB于点F,如果AB:AD=1:2,试判断四边形PEMF的形状,并说明理由.
如图,点M是平行四边形ABCD的边AD的中点,点P是边BC上的一个动点,PE∥MB,PF∥MC,分别交MC于点E、交MB于点F,如果AB:AD=1:2,试判断四边形PEMF的形状,并说明理由.
分析:先证四边形PEMF是平行四边形,再利用边之间的等量关系,易得AB=CD=AM=DM,再利用等边对等角,易得
∠ABM=∠AMB,∠DMC=∠DCM,结合四边形ABCD是?,易证∠CBM=∠ABM=
∠ABC,∠DCM=∠BCM=
∠DCB,
而∠ABC与∠DCB同旁内角互补易得∠MBC+∠MCB=90°,即∠BMC=90°,从而可证四边形PEMF为矩形.
∠ABM=∠AMB,∠DMC=∠DCM,结合四边形ABCD是?,易证∠CBM=∠ABM=
| 1 |
| 2 |
| 1 |
| 2 |
而∠ABC与∠DCB同旁内角互补易得∠MBC+∠MCB=90°,即∠BMC=90°,从而可证四边形PEMF为矩形.
解答:解:四边形PEMF为矩形;(1分)
∵PE∥MB,PF∥MC,
∴四边形PEMF为平行四边形,(3分)
∵平行四边形ABCD,
∴AB=CD,
∵M是边AD的中点,
∴AM=DM=
AD,
∵AB:AD=1:2,
∴AB=CD=AM=DM,(5分)
∴∠ABM=∠AMB,∠DMC=∠DCM,(6分)
∵AD∥CB,
∴∠CBM=∠AMB,∠DMC=∠BCM,(7分)
∴∠CBM=∠ABM=
∠ABC,∠DCM=∠BCM=
∠DCB,
∵AD∥CB,
∴∠ABC+∠DCB=180°,(9分)
∴∠MBC+∠MCB=90°,
∴∠BMC=90°,(10分)
∴平行四边形PEMF为矩形.(12分)
∵PE∥MB,PF∥MC,
∴四边形PEMF为平行四边形,(3分)
∵平行四边形ABCD,
∴AB=CD,
∵M是边AD的中点,
∴AM=DM=
| 1 |
| 2 |
∵AB:AD=1:2,
∴AB=CD=AM=DM,(5分)
∴∠ABM=∠AMB,∠DMC=∠DCM,(6分)
∵AD∥CB,
∴∠CBM=∠AMB,∠DMC=∠BCM,(7分)
∴∠CBM=∠ABM=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD∥CB,
∴∠ABC+∠DCB=180°,(9分)
∴∠MBC+∠MCB=90°,
∴∠BMC=90°,(10分)
∴平行四边形PEMF为矩形.(12分)
点评:本题利用了?的判定和性质、等边对等角、平行线的性质、矩形的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
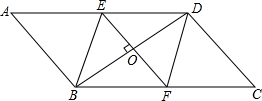 别交于点E、F.
别交于点E、F. 
 如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
