Question

【题目】如图，反比例函数y=（k＞0）与矩形OABC在第一象限相交于D、E两点，OA=2，OC=4，连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .

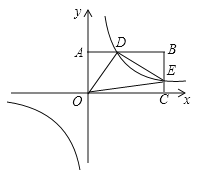
（1）①点B的坐标为 ；②S S（填“＞”、“＜”、“=”）；

（2）当点D为线段AB的中点时，求k的值及点E的坐标；

（3）当S+S=2时，试判断△ODE的形状，并求△ODE的面积.

Answer 1

【答案】（1）点B的坐标为（4,2），= ；

（2）k的值为4，点E的坐标为（4，1） ；

（3）△ODE为直角三角形，

【解析】

（1）根据OA=2，OC=4可直接得到点B坐标；②根据反比例函k的意义可知S1、S2都等于|k|，即可得到答案；
（2）当点D为AB中点时，AD=2，得出D的坐标是（2，2），，进而可得解；

（3）根据当S1+S2=2时，由（1）得出S1=S2=1，进而得出BD，BE的长，进而得出DO2+DE2=OE2，△ODE是直角三角形，进而得出三角形面积．

（1）矩形OABC，AB=OC，BC=OA；OA=2，OC=4，B点在第一象限

所以点B的坐标为（4,2）；

反比例函数y=（k＞0）与矩形OABC在第一象限相交于D、E两点，

设D、E两点的坐标分别为，

得；

D、E在第一象限， 记△OAD、△OCE的面积分别为、，，

所以=

（2）当点D为线段AB的中点时，D点的坐标（2，2），由（1）知，

解得k=4，

,

所以点E的坐标为（4，1）

(3) 当+S=2时，由（1）得;

=1，;;

在矩形OABC，BD=AB-AD=3；BE=BC-CE=；

都是直角三角形，由勾股定理得

∵

∴△ODE为直角三角形，

∴OD·DE=××