题目内容
【题目】如图,点![]() 在等边
在等边![]() 的边
的边![]() 上,
上,![]() ,射线
,射线![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是射线
是射线![]() 上一动点,点
上一动点,点![]() 是线段
是线段![]() 上一动点,当
上一动点,当![]() 的值最小时,
的值最小时,![]() ,则
,则![]() 的长为___________________.
的长为___________________.
【答案】13
【解析】
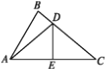
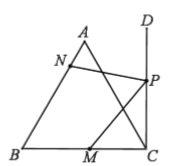
作出点M关于CD的对称点M1,然后过点M1作M1N⊥AB于N,交CD于点P,连接MP,根据对称性可得MP= M1P,MC= M1C,然后根据垂线段最短即可证出此时![]() 最小,然后根据等边三角形的性质可得AC=BC,∠B=60°,利用30°所对的直角边是斜边的一半即可求出BM1,然后求出BC即可求出AC.
最小,然后根据等边三角形的性质可得AC=BC,∠B=60°,利用30°所对的直角边是斜边的一半即可求出BM1,然后求出BC即可求出AC.
解:作出点M关于CD的对称点M1,然后过点M1作M1N⊥AB于N,交CD于点P,连接MP,如下图所示

根据对称性质可知:MP= M1P,MC= M1C
此时![]() =M1P+NP=M1N,根据垂线段最短可得此时
=M1P+NP=M1N,根据垂线段最短可得此时![]() 最小,且最小值为M1N的长
最小,且最小值为M1N的长
∵△ABC为等边三角形
∴AC=BC,∠B=60°
∴∠M1=90°-∠B=30°
∵![]() ,当
,当![]() 的值最小时,
的值最小时,![]() ,
,
∴在Rt△BM1N中,BM1=2BN=18
∴MM1= BM1-BM=10
∴MC= M1C=![]() MM1=5
MM1=5
∴BC=BM+MC=13
故答案为:13.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目