Question

【题目】如图，在平面直角坐标系中，以A(5，1)为圆心，2个单位长度为半径的⊙A交轴于点B、C．解答下列问题：

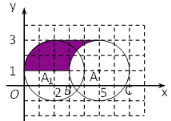
（1）将⊙A向下平移 个单位长度与轴相切；

（2） 将⊙A向左平移得到⊙A1，当⊙A1与轴首次相切，此时阴影部分的面积S＝ ；

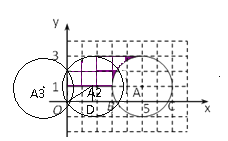
（3）将⊙A向左平移 个单位长度与坐标轴有三个公共点．

Answer 1

【答案】（1）3；（2）6；（3）3，，，7.

【解析】

（1）根据直角坐标系与相切的性质即可得到平移的距离；

（2）根据直线和圆相切的位置关系与数量之间的联系，得到A点坐标，再跟平移的性质即可求出阴影部分面积；

（3）由⊙A已经与x轴交于两点，故分圆与y轴相切与或圆过原点两种情况进行求解即可.

将⊙A向下平移3个单位长度与轴相切，

故填：3.

（2）根据直线和圆相切的位置关系与数量之间的联系，得点A′的坐标是（2，1）；

则移动的距离是52＝3；

根据平移变换的性质，则阴影部分的面积为3×2=6

故填：6；

（3）∵⊙A已经与x轴交于两点，

∴①圆与y轴相切

由圆心A的坐标为（5,1），2个单位长度为半径

故向左平移3或7个单位长度可与y轴相切；

②圆过原点时，如图⊙A2，作A2D⊥x轴于D点，连接A2O,

故OD=

此向左平移5-个单位长度，

同理可得平移至⊙A3时，平移距离为

综上故填：3，，，7.