题目内容
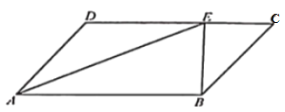
【题目】如图,AB是半径为2的⊙O的直径,直线l与AB所在直线垂直,垂足为C,OC=3,P是圆上异于A、B的动点,直线AP、BP分别交l于M、N两点.
(1)当∠A=30°时,MN的长是 ;
(2)求证:MCCN是定值;
(3)MN是否存在最大或最小值,若存在,请写出相应的最值,若不存在,请说明理由;
(4)以MN为直径的一系列圆是否经过一个定点,若是,请确定该定点的位置,若不是,请说明理由.

【答案】(1)![]() ;(2)MCNC=5;(3)a+b的最小值为2
;(2)MCNC=5;(3)a+b的最小值为2![]() ;(4)以MN为直径的一系列圆经过定点D,此定点D在直线AB上且CD的长为
;(4)以MN为直径的一系列圆经过定点D,此定点D在直线AB上且CD的长为![]() .
.
【解析】
(1)由题意得AO=OB=2、OC=3、AC=5、BC=1,根据MC=ACtan∠A=![]()
![]() 、CN=
、CN=![]() 可得答案;
可得答案;
(2)证△ACM∽△NCB得![]() ,由此即可求得答案;
,由此即可求得答案;
(3)设MC=a、NC=b,由(2)知ab=5,由P是圆上异于A、B的动点知a>0,可得b=![]() (a>0),根据反比例函数的性质得a+b不存在最大值,当a=b时,a+b最小,据此求解可得;
(a>0),根据反比例函数的性质得a+b不存在最大值,当a=b时,a+b最小,据此求解可得;
(4)设该圆与AC的交点为D,连接DM、DN,证△MDC∽△DNC得![]() ,即MCNC=DC2=5,即DC=
,即MCNC=DC2=5,即DC=![]() ,据此知以MN为直径的一系列圆经过定点D,此顶点D在直线AB上且CD的长为
,据此知以MN为直径的一系列圆经过定点D,此顶点D在直线AB上且CD的长为![]() .
.
(1)如图所示,根据题意知,AO=OB=2、OC=3,

则AC=OA+OC=5,BC=OC﹣OB=1,
∵AC⊥直线l,
∴∠ACM=∠ACN=90°,
∴MC=ACtan∠A=5×![]() =
=![]() ,
,
∵∠ABP=∠NBC,
∴∠BNC=∠A=30°,
∴CN= ,
,
则MN=MC+CN=![]() +
+![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)∵∠ACM=∠NCB=90°,∠A=∠BNC,
∴△ACM∽△NCB,
∴![]() ,
,
即MCNC=ACBC=5×1=5;
(3)设MC=a、NC=b,
由(2)知ab=5,
∵P是圆上异于A、B的动点,
∴a>0,
∴b=![]() (a>0),
(a>0),
根据反比例函数的性质知,a+b不存在最大值,当a=b时,a+b最小,
由a=b得a=![]() ,解之得a=
,解之得a=![]() (负值舍去),此时b=
(负值舍去),此时b=![]() ,
,
此时a+b的最小值为2![]() ;
;
(4)如图,设该圆与AC的交点为D,连接DM、DN,
∵MN为直径,
∴∠MDN=90°,
则∠MDC+∠NDC=90°,
∵∠DCM=∠DCN=90°,
∴∠MDC+∠DMC=90°,
∴∠NDC=∠DMC,
则△MDC∽△DNC,
∴![]() ,即MCNC=DC2,
,即MCNC=DC2,
由(2)知MCNC=5,
∴DC2=5,
∴DC=![]() ,
,
∴以MN为直径的一系列圆经过定点D,此定点D在直线AB上且CD的长为![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
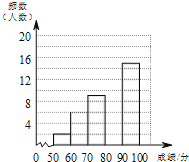
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?