题目内容
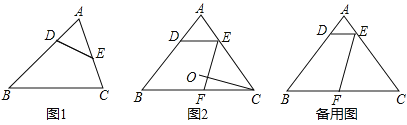
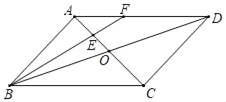
【题目】如图，在平行四边形ABCD中，AC、BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF＝3，则下列结论：①
；②S△BCE＝30；③S△ABE＝9；④△AEF∽△ACD，其中一定正确的是（ ）
A.①②③④B.①③C.②③④D.①②③
【答案】B
【解析】
根据平行四边形的性质得到AE＝
CE，根据相似三角形的性质得到比例式，等量代换得到AF＝AD，于是得到
；故①正确；根据相似三角形的性质得到S△BCE＝27；故②错误；根据三角形的面积公式得到S△ABE＝12，故③正确；由于△AEF与△ADC只有一个角相等，于是得到△AEF与△ACD不一定相似，故④错误．
解：∵在ABCD中，
，
∵点E是OA的中点，
，
∵AD∥BC，
∴△AFE∽△CBE，
，
∵AD＝BC，
，
；故①正确；
∵S△AEF＝3，
，
∴S△BCE＝27；故②错误；
∴S△ABE＝9，故③正确；
∵BF不平行于CD，
∴△AEF与△ADC只有一个角相等，
∴△AEF与△ACD不一定相似，故④错误，
故选B．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
