题目内容
如图在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB的中线,BC=2,将△ACM沿直线CM折叠点A落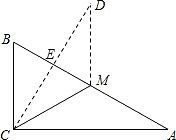 在点D处,如果CD恰好与AB垂直,垂足为点E,则DE的长为
在点D处,如果CD恰好与AB垂直,垂足为点E,则DE的长为分析:CM为斜边AB的中线,根据直角三角形斜边上的中线性质可知CM=BM=MA=MD,又∵CD⊥AB,故EM为等腰△CMD底边上的中线,即CE=ED,且EM平分∠CMD,即∠DME=∠CME=∠B,可证△EDM≌△ECB,则BC=DM,△BCM为等边三角形,DE=CE,在Rt△BCE中求CE即可.
解答:解:CM为Rt△ABC斜边AB的中线,
∴CM=BM=MA=MD,
又∵CD⊥AB,
∴EM为等腰△CMD底边上的中线,即CE=ED,
且EM平分∠CMD,即∠CMA=∠CMD=2∠CME,
而∠CMA+∠CME=180°,即2∠CME+∠CME=180°,
解得∠CME=60°,
∵CM=BM,△BCM为等边三角形,
在Rt△BCE中,CE=DE=BC•sin60°=
.
故答案为:
.
∴CM=BM=MA=MD,
又∵CD⊥AB,
∴EM为等腰△CMD底边上的中线,即CE=ED,
且EM平分∠CMD,即∠CMA=∠CMD=2∠CME,
而∠CMA+∠CME=180°,即2∠CME+∠CME=180°,
解得∠CME=60°,
∵CM=BM,△BCM为等边三角形,
在Rt△BCE中,CE=DE=BC•sin60°=
| 3 |
故答案为:
| 3 |
点评:本题考查了折叠的性质,直角三角形的性质及三角形全等的判定与性质.关键是通过推理得出等边三角形.

练习册系列答案
相关题目

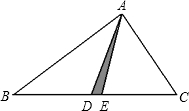 如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为
如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为 如图在Rt△ABC中,∠ACB=90°,sinA=
如图在Rt△ABC中,∠ACB=90°,sinA=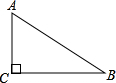 如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=
如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=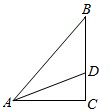 如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是
如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是 (1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=
(1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=