题目内容
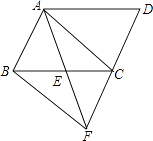
【题目】如图,已知O为直线AD上一点,射线OC,射线OB,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.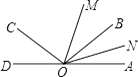
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
【答案】
(1)解:∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠DOC=180°,
∴∠COD=∠AOB;
(2)解:∵OM和ON分别是∠AOC和∠AOB的平分线,
∴∠AOM= ![]() ∠AOC,∠AON=
∠AOC,∠AON= ![]() ∠AOB,
∠AOB,
∴∠MON=∠AOM﹣∠AON= ![]() ∠AOC﹣
∠AOC﹣ ![]() ∠AOB=
∠AOB= ![]() (∠AOC﹣∠AOB)=
(∠AOC﹣∠AOB)= ![]() ∠BOC,
∠BOC,
∵∠MON=40°,
∴∠BOC=80°,
∴∠DOC+∠AOB=180°﹣80°=100°,
∵∠AOB=∠COD,
∴∠AOB=50°,
∴∠AOC=180°﹣∠COD=130°.
【解析】(1)根据题意可表示出∠AOC+∠AOB=180°,∠AOC+∠DOC=180°,由同角的补角相等可得答案;
(2)由OM和ON分别是∠AOC和∠AOB的平分线,可得到∠MON=![]() ∠BOC,进而求得∠BOC的度数,继而可得∠DOC+∠AOB的度数,再由(1)知,∠AOB=∠COD,则可得∠AOB的度数,又∠AOC=180°﹣∠COD可求出∠AOC的度数.
∠BOC,进而求得∠BOC的度数,继而可得∠DOC+∠AOB的度数,再由(1)知,∠AOB=∠COD,则可得∠AOB的度数,又∠AOC=180°﹣∠COD可求出∠AOC的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目