��Ŀ����
����Ŀ����1�����ⷢ��
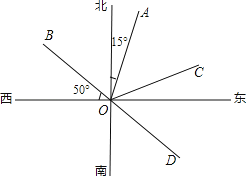
��ͼ1����ACB����DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ�����AEB�Ķ���Ϊ �����߶�AD��BE֮���������ϵΪ ��
��2����չ̽��
��ͼ2����ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����ж���AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�

���𰸡���1������AEB=60������AD=BE����2����AEB=90����AE=BE+2CM��
��������
�����������1����֤��ACD=��BCE��������֤��ACD�ա�BCE������ȫ�������ζ�Ӧ����ȿ����AD=BE������ȫ�������ζ�Ӧ����ȼ��������AEB�Ĵ�С��
��2����֤��ACD����BCE���ɵ���ADC=��BEC���������������AEB=90�����������DM=ME=CM�����ɽ��⣮
�⣺��1���ߡ�ACB=��DCE����DCB=��DCB��
���ACD=��BCE��
����ACD����BCE��
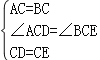 ��
��
���ACD�ա�BCE��SAS����
��AD=BE����CEB=��ADC=180������CDE=120����
���AEB=��CEB����CED=60����
��2����AEB=90����AE=BE+2CM��
���ɣ���ͼ2��
�ߡ�ACB����DCE��Ϊ����ֱ�������Σ�
��CA=CB��CD=CE����ACB=��DCE=90�㣬
���ACD=��BCE��
����ACD����BCE��
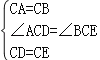 ��
��
���ACD�ա�BCE��SAS����
��AD=BE����ADC=��BEC��
�ߡ�DCEΪ����ֱ�������Σ�
���CDE=��CED=45����
����A��D��E��ͬһֱ���ϣ�
���ADC=135����
���BEC=135����
���AEB=��BEC����CED=90����
��CD=CE��CM��DE��
��DM=ME��
�ߡ�DCE=90����
��DM=ME=CM��
��AE=AD+DE=BE+2CM��

����Ŀ��ij��˾����һ�ֽ���Ϊ20 ��Ԫ/�����ļ���������������y ������������ۼ۸�x ��Ԫ/����֮��Ϊһ�κ�����ϵ����仯���±���
�۸�x ��Ԫ/���� | �� | 30 | 50 | �� |
������y ������� | �� | 5 | 3 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ�����ù�˾Ҫ���40��Ԫ�ľ������Ҿ������ù˿͵õ�ʵ�ݣ���ô���ۼ۸�Ӧ��Ϊ���٣�
��ע��������=�����۶�ܽ��۩�������֧��