题目内容
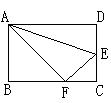
矩形ABCD,折叠矩形的一边AD,使点D落在BC边的点F处,已知折痕AE=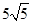 cm,且tan∠EFC=
cm,且tan∠EFC=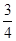 。
。
(1)求证:△AFB∽△FEC;
(2)求矩形ABCD的周长。
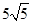 cm,且tan∠EFC=
cm,且tan∠EFC=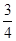 。
。(1)求证:△AFB∽△FEC;
(2)求矩形ABCD的周长。

(1)略 (2)36cm
(1)证明:∵∠AFE=90°,∠B=90°,∠C=90°.
∴∠BAF+∠AFB=∠AFB+∠EFC=∠EFC+∠FEC=90°.
∴∠BAF=∠EFC,∠AFB=∠FEC.
∴△AFB∽△FEC.
(2)设CE=3k,则CF=4k,由勾股定理得EF=DE=5k,
∴DC=AB=8k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC=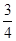
∴BF=6k,AF=BC=AD=10k,
在Rt△AFE中由勾股定理得AE= =5
=5
解得:k=1,
故矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36cm.
(1)矩形的特点是四个角均为直角,折叠的部分所包含的角也是直角,利用在直角三角形中两锐角互余可得∠BAF=∠CFE,进而可证明△ABF∽△FCE;
(2)利用相似三角形对应边成比例,再利用勾股定理即可得解.
∴∠BAF+∠AFB=∠AFB+∠EFC=∠EFC+∠FEC=90°.
∴∠BAF=∠EFC,∠AFB=∠FEC.
∴△AFB∽△FEC.
(2)设CE=3k,则CF=4k,由勾股定理得EF=DE=5k,
∴DC=AB=8k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC=
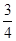
∴BF=6k,AF=BC=AD=10k,
在Rt△AFE中由勾股定理得AE=
 =5
=5
解得:k=1,
故矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36cm.
(1)矩形的特点是四个角均为直角,折叠的部分所包含的角也是直角,利用在直角三角形中两锐角互余可得∠BAF=∠CFE,进而可证明△ABF∽△FCE;
(2)利用相似三角形对应边成比例,再利用勾股定理即可得解.

练习册系列答案
相关题目
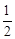 AC的长为半径在AC的两边作弧,交于点M、N;②连接MN,分别交AB、AC于点D、O;③过点C作CE∥AB交MN于点E,连接AE、CD.
AC的长为半径在AC的两边作弧,交于点M、N;②连接MN,分别交AB、AC于点D、O;③过点C作CE∥AB交MN于点E,连接AE、CD.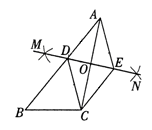
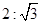
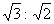
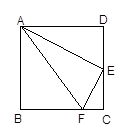
 中,
中, ,
, ,
,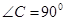 .
.
 ,使
,使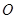 为对称中心,并且以直线
为对称中心,并且以直线 为对称轴的图案.
为对称轴的图案.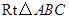 中,
中, .
.
 的平分线
的平分线 交
交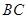 于点
于点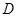 (只保留作图痕迹,不写作法);
(只保留作图痕迹,不写作法);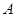 与点
与点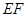 交
交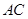 于点
于点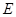 ,交
,交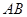 于点
于点 ,连接
,连接 ,再展回到原图形,得到四边形
,再展回到原图形,得到四边形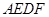 .
.