题目内容
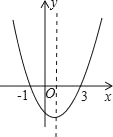
【题目】在一个不透明的盒子里装有4个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字为m,点P的坐标为(m,m2+1),则点P落在抛物线y=﹣4x2+8x+5与x轴所围成的区域内(含边界)的概率是___.
【答案】![]() .
.
【解析】
画出抛物线图象,确定各点横坐标所对应的纵坐标,与P点纵坐标比较即可.
如图,

当m=-2,-1,0,1,2时,m2+1=5,2,1,2,5,
则点P的坐标为(-2,5),(-1,2),(0,1),(1,2),(2,5);
描出各点:-2<-0.5,-1<-0.5,不合题意;
把x=0代入解析式得:y1=5,1<5,故(0,1)在该区域内;
把x=1代入解析式得:y2=9,2<9,故(1,2)在该区域内;
把x=2代入解析式得:y3=5,5=5,故(2,5)在边界上,在该区域内.
所以5个点中有3个符合题意,
点P落在抛物线y=-4x2+8x+5与x轴所围成的区域内(含边界)的概率是![]() .
.
故答案为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目