题目内容
作△ABC关于直线l对称的△A′B′C′，点A，B，C的对称点分别是A′，B′，C′，则下列说法中正确的是（ ）
分析：根据轴对称图形的性质分别分析得出即可．
解答：解：∵△ABC关于直线l对称的△A′B′C′，点A，B，C的对称点分别是A′，B′，C′，
∴对称轴垂直平分AA′，故选项A错误；
△ABC和△A′B′C′的周长相等，故选项B正确，
线段BB′被对称轴平分，故选项C错误；
△ABC与△A′B′C′关于对称轴对称，不可能△ABC的面积被对称轴平分，故选项D错误．
故选：B．
∴对称轴垂直平分AA′，故选项A错误；
△ABC和△A′B′C′的周长相等，故选项B正确，
线段BB′被对称轴平分，故选项C错误；
△ABC与△A′B′C′关于对称轴对称，不可能△ABC的面积被对称轴平分，故选项D错误．
故选：B．
点评：本题考查了轴对称的性质，熟练掌握轴对称图形的性质是解题的关键．
练习册系列答案
相关题目
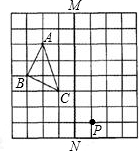如图，在正方形网格上的一个△ABC．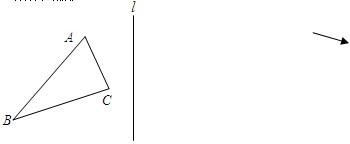
（2013•重庆）作图题：（不要求写作法）如图，△ABC在平面直角坐标系中，其中，点A、B、C的坐标分别为A（-2，1），B（-4，5），C（-5，2）．
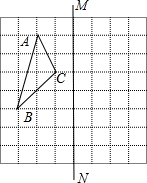（1）作△ABC关于直线MN对称的△A′B′C′．
在如图的正方形网格中有一个三角形ABC．