题目内容
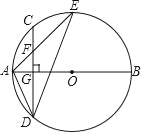
【题目】如图,在扇形MON中,圆心角∠MON=60°,边长为2的菱形OABC的顶点A,C,B分别在ON,OM和![]() 上,且ND∥AB,交CB的延长线于点D,则阴影部分的面积是_____.
上,且ND∥AB,交CB的延长线于点D,则阴影部分的面积是_____.
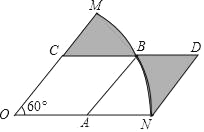
【答案】6﹣2![]()
【解析】
由扇形的面积计算公式结合三角形、平行四边形的面积计算公式计算即可.
解:如图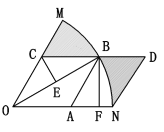
连接OB,过C点做OB的垂线,垂足为E点,
由四边形OABC为菱形,∠MON=60°,可得∠COB=∠BOA=![]() ∠COA=
∠COA=![]() ,
,
可得![]() ,
,![]() ,
,
在RT△OCE中,OC=2, ∠COB=![]() ,可得CE=1,OE=
,可得CE=1,OE=![]() ,则OB=
,则OB=![]() ,即圆的半径为
,即圆的半径为![]() ,
,
可得:![]() =
=![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
![]() 阴影部分的面积即为四边形ABDN的面积,
阴影部分的面积即为四边形ABDN的面积,
由BD∥AN,AB∥DN,
可得四边形ABDN为平行四边形,
过点B做BF⊥AN,可得BF=![]() ,
,
![]()
![]() ,
,
故阴影部分的面积为![]() .
.

练习册系列答案
相关题目
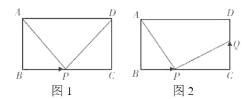
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )

A. 115° B. 105° C. 95° D. 85°
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?