��Ŀ����
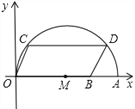
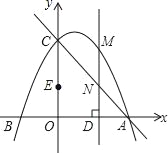
����Ŀ����ͼ��������y=��![]() +bx+c����A��4��0����C��0��4�����㣬��B����������x�����һ�����㣬��E��OC���е㣬��ֱ��AC����M���������ϣ�����M��MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N�����M�ĺ�����Ϊm��MN�ij���Ϊd��
+bx+c����A��4��0����C��0��4�����㣬��B����������x�����һ�����㣬��E��OC���е㣬��ֱ��AC����M���������ϣ�����M��MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N�����M�ĺ�����Ϊm��MN�ij���Ϊd��
��1��ֱ��д��ֱ��AC�ĺ�����ϵʽ��
��2���������߶�Ӧ�ĺ�����ϵʽ��
��3����d����m�ĺ�����ϵʽ��
��4�����Ե�M��N��E��OΪ������ı���Ϊƽ���ı���ʱ��ֱ��д��m��ֵ��
���𰸡���1��y=��x+4��2��y=��![]() x2+x+4��3����������4�����Ե�M��N��E��OΪ������ı���Ϊƽ���ı���ʱ��m��ֵΪm1=2��m2=2��2
x2+x+4��3����������4�����Ե�M��N��E��OΪ������ı���Ϊƽ���ı���ʱ��m��ֵΪm1=2��m2=2��2![]() ��m3=2+2
��m3=2+2![]() ��
��
��������
��1�����ݴ���ϵ�������ɵ�ֱ�ߵĽ���ʽ��
��2�����ݴ���ϵ�������ɵ������ߵĽ���ʽ��
��3������ƽ����y���ֱ���������ľ����Ǵ���������С�������꣬�ɵô𰸣�
��4������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��ɵ�MN�ij������ݽⷽ�̣��ɵô𰸣�
��1����ֱ��AC�Ľ���ʽΪy=kx+b����A��C���������룬��
![]()
���![]()
ֱ��AC�Ľ���ʽΪy=��x+4��
��2����A��C��������������ߵĽ���ʽ����

���![]()
�����ߵĽ���ʽΪ![]()
��3���ߵ�M�ĺ�����Ϊm��
��M�������Ϊ![]() ��N������Ϊ��m����m+4����
��N��������m����m+4����
�ٵ���M�ڵ�N���Ϸ�ʱ�� ![]()
![]()
�ڵ���M�ڵ�N���·�ʱ�� ![]()
![]()
��4��m��ֵΪ![]()
�������£�
�ٵ�M�ڵ�N���Ϸ�ʱ��MN�TOE=2����![]()
���m1=m2=2��
��m=2��
�ڵ���M�ڵ�N���·�ʱ��MN=OE=2����![]()
���![]()
��![]()
�������������Ե�M��N��E��OΪ������ı���Ϊƽ���ı���ʱ��m��ֵΪm1=2��![]()

 ��У����ϵ�д�
��У����ϵ�д�