题目内容
设△ABC的面积为1,D是边AB上一点,且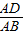 =
= ,若在边AC上取一点E,使四边形DECB的面积为
,若在边AC上取一点E,使四边形DECB的面积为 ,则
,则 的值为( )
的值为( )A.

B.

C.

D.

【答案】分析:连接BE.要求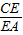 的值,根据三角形的面积公式,即求△ABE和△BCE的面积比.根据
的值,根据三角形的面积公式,即求△ABE和△BCE的面积比.根据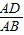 =
= ,得△ADE和△ABE的面积比是1:3,设△ADE的面积是k,则△ABE的面积是3k,则△BDE的面积是2k,设△BCE的面积是x,则有(2k+x)=
,得△ADE和△ABE的面积比是1:3,设△ADE的面积是k,则△ABE的面积是3k,则△BDE的面积是2k,设△BCE的面积是x,则有(2k+x)= (3k+x),解得x=k,从而求得△ABE和△BCE的面积比是3:1,即可求解.
(3k+x),解得x=k,从而求得△ABE和△BCE的面积比是3:1,即可求解.
解答: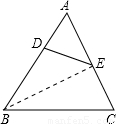 解:连接BE.
解:连接BE.
∵ =
= ,
,
∴△ADE和△ABE的面积比是1:3.
设△ADE的面积是k,则△ABE的面积是3k,则△BDE的面积是2k.
设△BCE的面积是x,则有(2k+x)= (3k+x),
(3k+x),
解得x=k.
则△ABE和△BCE的面积比是3:1,
则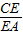 的值为
的值为 .
.
故选B.
点评:此题考查了等高的两个三角形的面积比即为它们的底的比.
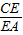 的值,根据三角形的面积公式,即求△ABE和△BCE的面积比.根据
的值,根据三角形的面积公式,即求△ABE和△BCE的面积比.根据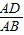 =
= ,得△ADE和△ABE的面积比是1:3,设△ADE的面积是k,则△ABE的面积是3k,则△BDE的面积是2k,设△BCE的面积是x,则有(2k+x)=
,得△ADE和△ABE的面积比是1:3,设△ADE的面积是k,则△ABE的面积是3k,则△BDE的面积是2k,设△BCE的面积是x,则有(2k+x)= (3k+x),解得x=k,从而求得△ABE和△BCE的面积比是3:1,即可求解.
(3k+x),解得x=k,从而求得△ABE和△BCE的面积比是3:1,即可求解.解答:
 解:连接BE.
解:连接BE.∵
 =
= ,
,∴△ADE和△ABE的面积比是1:3.
设△ADE的面积是k,则△ABE的面积是3k,则△BDE的面积是2k.
设△BCE的面积是x,则有(2k+x)=
 (3k+x),
(3k+x),解得x=k.
则△ABE和△BCE的面积比是3:1,
则
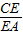 的值为
的值为 .
.故选B.
点评:此题考查了等高的两个三角形的面积比即为它们的底的比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
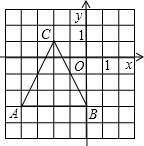 已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( )
已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( )| A、S1>S2 | B、S1=S2 | C、S1<S2 | D、不能确定 |
设△ABC的面积为1,D是边AB上一点,且
=
,若在边AC上取一点E,使四边形DECB的面积为
,则
的值为( )
| AD |
| AB |
| 1 |
| 3 |
| 3 |
| 4 |
| CE |
| EA |
A、
| ||
B、
| ||
C、
| ||
D、
|
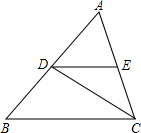 已知:如图,△ABC中,AB=4,D是AB边上的一个动点,DE∥BC,连接DC,设△ABC的面积为S,△DCE的面积为S′.
已知:如图,△ABC中,AB=4,D是AB边上的一个动点,DE∥BC,连接DC,设△ABC的面积为S,△DCE的面积为S′.