题目内容
若在△ABC和△DEF中,已知边AB=5,AC=6,DE=6,DF=8,三角形的内角∠A=50°,∠B=70°,∠D=40°,∠E=120°,若设△ABC的面积为S1,△DEF的面积为S2,则s1+s2等于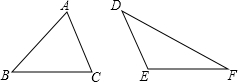
分析:先根据∠A=50°,∠B=70°可求出∠C的度数,再AC=6,DE=6,∠A=50°,∠D=40°,∠E=120°可知,若把AC与DE重合则△ABF恰好构成直角三角形,再利用三角形的面积公式即可求解.
解答: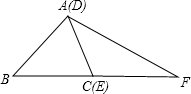 解:∵△ABC中,∠A=50°,∠B=70°,
解:∵△ABC中,∠A=50°,∠B=70°,
∴∠C=180°-∠A-∠B=180°-50°-70°=60°,
∵AC=6,DE=6,∠A=50°,∠D=40°,∠E=120°,
∴若把AC与DE重合则△ABF恰好构成直角三角形(如图所示),
∴s1+s2=s△ABF=
AB•DF=
×5×8=20.
故答案为:20.
 解:∵△ABC中,∠A=50°,∠B=70°,
解:∵△ABC中,∠A=50°,∠B=70°,∴∠C=180°-∠A-∠B=180°-50°-70°=60°,
∵AC=6,DE=6,∠A=50°,∠D=40°,∠E=120°,
∴若把AC与DE重合则△ABF恰好构成直角三角形(如图所示),
∴s1+s2=s△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:20.
点评:本题考查的是三角形的面积及三角形内角和定理,解答此题时不要盲目求解,要注意观察两三角形的特点,能根据两三角形的边长及各角的度数,判断出若把AC与DE重合,则△ABF恰好构成直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
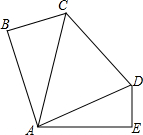 (2007•西城区一模)农科所有一块五边形的实验田,用于种植1号良种水稻进行实验,如图所示,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20米,
(2007•西城区一模)农科所有一块五边形的实验田,用于种植1号良种水稻进行实验,如图所示,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20米,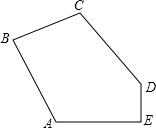 有一块五边形的试验田,用于种植1号良种水稻进行实验,如图所示,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20米.
有一块五边形的试验田,用于种植1号良种水稻进行实验,如图所示,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20米.
 ,△DEF的面积为
,△DEF的面积为 ,则
,则 等于 ▲
。
等于 ▲
。