题目内容
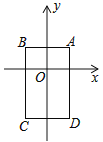
【题目】如图正比例函数y=k1x与反比例函数![]() 交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
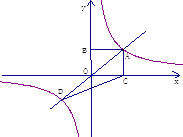
(1)分别求出正比例函数与反比例函数的解析式;
(2)求出正、反比例函数图象的另外一个交点坐标。
(3)求△ODC的面积.
【答案】(1)正比例函数的解析式是y=x;反比例函数的解析式是y=![]() ;
;
(2)另一个交点的坐标为(2,2);
(3)S△ODC=2.
【解析】试题分析:(1)由正方形的面积可得点A的坐标(2,2),则代入正比例函数y=k1x,反比例函数y2=![]() ,求得函数解析式.
,求得函数解析式.
(2)根据A、D两点关于原点对称可以确定出D点坐标.
(3)由O、C、D三点坐标可得△ODC的面积.
试题解析:(1)设正比例函数y1=k1x,反比例函数y2=![]() ,
,
由正方形的面积可得点A的坐标(2,2),代入两函数表达式可得:k1=1,k2=4.
则正比例函数的解析式为y1=x;反比例函数的解析式为y2=![]() ;
;
(2)∵正、反比例函数图象的另外一个交点是D,且点D和点A关于坐标原点对称,
∵A点坐标为(2,2),
∴D点坐标为(2,2).
即另一个交点的坐标为(2,2).
(3)∵△ODC是以A点横坐标的绝对值为底边,以D点纵坐标的绝对值为高,
∴S△ODC=![]() ×|xA|×|yD|=2.
×|xA|×|yD|=2.

练习册系列答案
相关题目