题目内容
今年我市水果大丰收,A、B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基础运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件。
(1)设从A基础运往甲 销售点水果x件,总运费为w元,请用含x的代数式表示w,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费。
(1)设从A基础运往甲 销售点水果x件,总运费为w元,请用含x的代数式表示w,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费。
解:(1)80≤x≤380
(2)x=200时,运费w最低,最低运费为81200元。
此时运输方案如下:
(2)x=200时,运费w最低,最低运费为81200元。
此时运输方案如下:
| | A | B |
| 甲 | 200 | 200 |
| 乙 | 180 | 120 |
试题分析:(1)用x表示出从A基地运往乙销售点的水果件数,从B基地运往甲、乙两个销售点的水果件数,然后根据运费=单价×数量列式整理即可得解,再根据运输水果的数量不小于0列出不等式求解得到x的取值范围;(2)根据一次函数的增减性确定出运费最低时的运输方案,然后求解即可.
试题解析:
(1)依题意,列表得
| | A(380) | B(320) |
| 甲(400) | x | 400-x |
| 乙(300) | 380-x | 320-(400-x)=x-80 |
∴W=40x+20×(380-x)+15×(400-x)+30×(x-80)=35x+11200
又
 解得80≤x≤380
解得80≤x≤380(2) 依题意得
 解得
解得 ,∴x=200,201,202
,∴x=200,201,202因w=35x+10,k=35,w随x的增大而增大,所以x=200时,运费w最低,最低运费为81200元。
此时运输方案如下:
| | A | B |
| 甲 | 200 | 200 |
| 乙 | 180 | 120 |

练习册系列答案
相关题目
 的整数解.
的整数解.

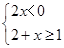 的解集在数轴上表示为( )
的解集在数轴上表示为( )