题目内容

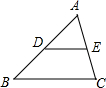如图，点D、E分别是△ABC的边AB、AC的中点，
求证：DE∥BC，且DE= $数学公式$ BC（提示仅供参考：延长DE至点F，使EF=DE，…）

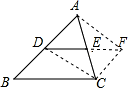证明：延长DE到点F，使EF=DE，连接FC、DC、AF，
∵AE=EC，
∴四边形ADCF是平行四边形，
CF平行且等于DA，
∴四边形DBCF是平行四边形，
DF平行且等于BC
又∵DE= $\text{[math]}$ DF，
∴DE∥BC，且DE= $\text{[math]}$ ．
分析：延长DE到点F，使EF=DE，连接FC、DC、AF，利用平行四边形的对边平行且相等可以证明结论．
点评：此题考查了三角形的中位线定理的数量关系，熟练掌握定理是解题的关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

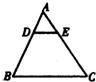17、如图，点D、E分别是△ABC边AB、AC上的点，且DE∥BC，BD=2AD，那么△ADE的周长：△ABC的周长=

如图，点D，E分别是矩形OABC中AB和BC边上的中点，点B的坐标为（6，4）
（1）写出A，C，E，D四点的坐标；并判断点O到直线DE的距离是否等于线段的OE长；
（2）动点F在线段DE上，FG⊥x轴于G，FH⊥y轴于H，求矩形面积最大时点F的坐标（利用图1解答）；
（3）我们给出如下定义：分别过抛物向上的两点（不在x轴上）作x轴的垂线，如果以这两点及垂足为顶点的矩形在这条抛物线与x轴围成的封闭图形内部，则称这个矩形是这条抛物线的内接矩形，请你理解上述定义，解答下面的问题：若矩形OABC是某个抛物线的周长最大的内接矩形，求这个抛物线的解析式（利用图2解答）．

如图，点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点，且
BE=CD，DB的延长线交AE于点F，则图1中∠AFB的度数为

；若将条件“正三角形、正四边形、正五边形”改为“正n边形”，其他条件不变，则∠AFB的度数为

．（用n的代数式表示，其中，n≥3，且n为整数）

（2013•武汉模拟）如图，点I和O分别是△ABC的内心和外心，则∠AIB和∠AOB的关系为（　　）

A．∠AIB=∠AOB

B．∠AIB≠∠AOB

如图，点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点，且BE=CD，DB延长线交于AE于点F，则∠AFB的度数是