��Ŀ����
��ͼ����D��E�ֱ��Ǿ���OABC��AB��BC���ϵ��е㣬��B������Ϊ��6��4����1��д��A��C��E��D�ĵ�����ꣻ���жϵ�O��ֱ��DE�ľ����Ƿ�����߶ε�OE����
��2������F���߶�DE�ϣ�FG��x����G��FH��y����H�������������ʱ��F�����꣨����ͼ1��𣩣�
��3�����Ǹ������¶��壺�ֱ���������ϵ����㣨����x���ϣ���x��Ĵ��ߣ�����������㼰����Ϊ����ľ�����������������x��Χ�ɵķ��ͼ���ڲ������������������������ߵ��ڽӾ��Σ����������������壬�����������⣺������OABC��ij�������ߵ��ܳ������ڽӾ��Σ�����������ߵĽ���ʽ������ͼ2��𣩣�
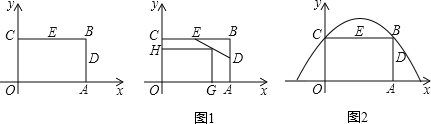
��������1�����ݾ��ε����ʺ�B������꣬�����A��C��D��E�����꣬��֪��CE=BE=3��BD=2�������ԡ�CDE�͡�BDE�����ƣ���ˡ�CED�١�BDE��Ҳ����˵��CED+��BED��90�㣬OE��DE����ֱ�����O��ED�ľ��벻����OE�ij���
��2�����ε����ʵ������F���������������ij˻���������ֱ��DE�Ľ���ʽ�ǽ���Ĺؼ����ɸ��ݣ�1���ó���D��E���������ֱ��DE�Ľ���ʽ�������ɸ��ݾ��ε������ʽ�ó����ε����S��F������ĺ�����ϵʽ�����ݺ��������ʼ������S�����ֵ����Ӧ��F�����ꣻ
��3��������ȸ���B��C��������������ߵĽ���ʽ��ʹ�����ߵĴ���ϵ��ֻ�ж�����һ�������������SPQR�������ߵ������ڽӾ��Σ�R��S���������ϣ����ɸ��������ߵĽ���ʽ���R��S�����꣬���ɱ�ʾ��RS��RP�ij���Ȼ����ݾ����ܳ��ļ��㷽���ɵó����ھ����ܳ���R��S����һ�������ĺ�����ϵʽ�����и������������ڽӾ��ε��ܳ����ʱ��xӦ��Ϊ6����˵ó��ĺ����ĶԳ��ἴΪx=6���ɴ˿�ȷ�������ߵĶ�����ϵ����ֵ��
��2�����ε����ʵ������F���������������ij˻���������ֱ��DE�Ľ���ʽ�ǽ���Ĺؼ����ɸ��ݣ�1���ó���D��E���������ֱ��DE�Ľ���ʽ�������ɸ��ݾ��ε������ʽ�ó����ε����S��F������ĺ�����ϵʽ�����ݺ��������ʼ������S�����ֵ����Ӧ��F�����ꣻ
��3��������ȸ���B��C��������������ߵĽ���ʽ��ʹ�����ߵĴ���ϵ��ֻ�ж�����һ�������������SPQR�������ߵ������ڽӾ��Σ�R��S���������ϣ����ɸ��������ߵĽ���ʽ���R��S�����꣬���ɱ�ʾ��RS��RP�ij���Ȼ����ݾ����ܳ��ļ��㷽���ɵó����ھ����ܳ���R��S����һ�������ĺ�����ϵʽ�����и������������ڽӾ��ε��ܳ����ʱ��xӦ��Ϊ6����˵ó��ĺ����ĶԳ��ἴΪx=6���ɴ˿�ȷ�������ߵĶ�����ϵ����ֵ��
����⣺��1��A��6��0����D��6��2����E��3��4����C��0��4��
�𣺲�����
���ɣ�����OE��OD��ED��
��OE2=25��ED2=13��OD2=40
��OE2+ED2��OD2
��OE��DE����ֱ����O��ֱ��ED�ľ��벻���߶�OE�ij���
��֤�������ܶ࣬�١�ODE�����Ϊ9�����DE���ϵĸ�h=
��OE=5�ij��Ƚϣ�
����ֱ��DE��x��y��Χ�ɵ��������У����õȻ��������O��ֱ��DE�ľ���
��OE�Ƚϣ�
��֤����ODE�͡�EBD�����ƣ����OED��90�㣻
���ӳ�ED��x����P����Rt��DAP�У�tan��EPO=2��3�����ڡ�QEP�У�OE��EP��2��3�����OED��90�㣮��
��2���ⷨһ��
�ӳ�ED��x���ڵ�H������֪�á�EBD�ա�HAD��
��AH=EB=3
��HO=9��OG=m����HG=9-m��
�ɡ�HAD�ס�HGF�ɵ�
=
��
=
��GF=
��9-m��=-
m+6
S����OGFH=OG•GF=m��-
m+6��=-
m2+6m��3��m��6��
��m=-
=-
=
ʱ��S����OGFH���
GF=-
��
+6=3
���F��
��3����
�ⷨ������ֱ��ED�Ľ���ʽΪy=kx+b����ͼ��E��D����ɵã�
��
���
��
��y=-
x+6
���F������ΪF��m��n����
�ɵ�F���߶�ED�Ͽɵã�n=-
m+6
��FG��x���ڵ�G��FH��y���ڵ�H��
��FG=n��FH=m
��S����OGFH=mn=m��-
m+6��=-
m2+6m��3��m��6��
��m=-
��m=-
=-
=
ʱ��S����OGFH���
GF=-
��
+6=3
���F��
��3��
��3������������ߵĽ���ʽΪy=ax2+bx+c��a��0�����ڽӾ��εĶ����֪��
�������߾���B��C���㣬�Գ���x=-
=3����c=4
����������ߵĽ���ʽΪy=ax2-6ax+4
��ͼ�������SPQR����������ߵ���һ�ڽӾ��Σ��ҵ�R��x��y���ɶԳ��Կ�֪��S��6-x��y��
��RS=2x-6��RQ=y
�֡ߵ�R������������ϣ�
��y=ax2-6ax+4
��C����SPQR=2��2x-6+y��
=2��2x-6+ax2-6ax+4��=2ax2+��-4-12a��x-4
��֪��֪��x=6ʱ��C����SPQRȡ�����ֵ��
��-4-12a=
a
��a=-
��ˣ����������ߵĽ���ʽΪy=-
x2+2x+4��
�𣺲�����
���ɣ�����OE��OD��ED��
��OE2=25��ED2=13��OD2=40
��OE2+ED2��OD2
��OE��DE����ֱ����O��ֱ��ED�ľ��벻���߶�OE�ij���
��֤�������ܶ࣬�١�ODE�����Ϊ9�����DE���ϵĸ�h=
18
| ||
| 13 |
����ֱ��DE��x��y��Χ�ɵ��������У����õȻ��������O��ֱ��DE�ľ���
18
| ||
| 13 |
��֤����ODE�͡�EBD�����ƣ����OED��90�㣻
���ӳ�ED��x����P����Rt��DAP�У�tan��EPO=2��3�����ڡ�QEP�У�OE��EP��2��3�����OED��90�㣮��
��2���ⷨһ��
�ӳ�ED��x���ڵ�H������֪�á�EBD�ա�HAD��
��AH=EB=3
��HO=9��OG=m����HG=9-m��
�ɡ�HAD�ס�HGF�ɵ�
| HA |
| HG |
| AD |
| GF |
| 3 |
| 9-m |
| 2 |
| GF |
��GF=
| 2 |
| 3 |
| 2 |
| 3 |
S����OGFH=OG•GF=m��-
| 2 |
| 3 |
| 2 |
| 3 |
��m=-
| b |
| 2a |
| 6 | ||
2��(-
|
| 9 |
| 2 |
GF=-
| 2 |
| 3 |
| 9 |
| 2 |
���F��
| 9 |
| 2 |
�ⷨ������ֱ��ED�Ľ���ʽΪy=kx+b����ͼ��E��D����ɵã�
|
���
|
��y=-
| 2 |
| 3 |
���F������ΪF��m��n����
�ɵ�F���߶�ED�Ͽɵã�n=-
| 2 |
| 3 |
��FG��x���ڵ�G��FH��y���ڵ�H��
��FG=n��FH=m
��S����OGFH=mn=m��-
| 2 |
| 3 |
| 2 |
| 3 |
��m=-
| b |
| 2a |
| b |
| 2a |
| 6 | ||
2��(-
|
| 9 |
| 2 |
GF=-
| 2 |
| 3 |
| 9 |
| 2 |
���F��
| 9 |
| 2 |
��3������������ߵĽ���ʽΪy=ax2+bx+c��a��0�����ڽӾ��εĶ����֪��
�������߾���B��C���㣬�Գ���x=-
| b |
| 2a |
����������ߵĽ���ʽΪy=ax2-6ax+4
��ͼ�������SPQR����������ߵ���һ�ڽӾ��Σ��ҵ�R��x��y���ɶԳ��Կ�֪��S��6-x��y��
��RS=2x-6��RQ=y
�֡ߵ�R������������ϣ�
��y=ax2-6ax+4
��C����SPQR=2��2x-6+y��
=2��2x-6+ax2-6ax+4��=2ax2+��-4-12a��x-4
��֪��֪��x=6ʱ��C����SPQRȡ�����ֵ��
��-4-12a=
| 2 |
| 3 |
��a=-
| 1 |
| 3 |
��ˣ����������ߵĽ���ʽΪy=-
| 1 |
| 3 |
���������⿼���˾��ε����ʡ����κ�����Ӧ�õ�֪ʶ���ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
 17����ͼ����D��E�ֱ��ǡ�ABC��AB��AC�ϵĵ㣬��DE��BC��BD=2AD����ô��ADE���ܳ�����ABC���ܳ�=
17����ͼ����D��E�ֱ��ǡ�ABC��AB��AC�ϵĵ㣬��DE��BC��BD=2AD����ô��ADE���ܳ�����ABC���ܳ�=
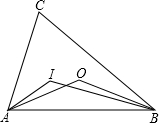 ��2013•�人ģ�⣩��ͼ����I��O�ֱ��ǡ�ABC�����ĺ����ģ����AIB�͡�AOB�Ĺ�ϵΪ��������
��2013•�人ģ�⣩��ͼ����I��O�ֱ��ǡ�ABC�����ĺ����ģ����AIB�͡�AOB�Ĺ�ϵΪ��������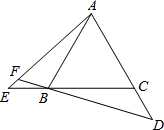 ��ͼ����E��D�ֱ�����������ABC����C��Ϊ�����һ���ӳ��ߺ���һ�߷����ӳ����ϵĵ㣬��BE=CD��DB�ӳ��߽���AE�ڵ�F�����AFB�Ķ�����
��ͼ����E��D�ֱ�����������ABC����C��Ϊ�����һ���ӳ��ߺ���һ�߷����ӳ����ϵĵ㣬��BE=CD��DB�ӳ��߽���AE�ڵ�F�����AFB�Ķ�����