题目内容
如图,点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB的延长线交AE于点F,则图1中∠AFB的度数为
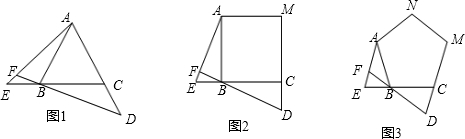
分析:分别求出正三角形、正四边形、正五边形时∠AFB的度数,找出规律即可解答.
解答:解:(1)在正△ABC中,AB=BC,∠ABC=∠ACB=60°
∴∠ABE=∠BCD=120°,
又∵BE=CD,
∴△ABE≌△BCD,
∴∠E=∠D
又∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°
(2)由以上不难得:△AEB≌△BDC进一步证出,△BEF∽△BDC,
得出,∠AFB的度数等于∠DCB=90°,同理可得:∠AFB度数为108°
(3)由正三角形、正四边形、正五边形时,∠AFB的度数分别为60°,90°,108°,可得出“正n边形”,其它条件不变,则∠AFB度数为
.
故填:60°;
.
∴∠ABE=∠BCD=120°,
又∵BE=CD,
∴△ABE≌△BCD,
∴∠E=∠D
又∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°
(2)由以上不难得:△AEB≌△BDC进一步证出,△BEF∽△BDC,
得出,∠AFB的度数等于∠DCB=90°,同理可得:∠AFB度数为108°
(3)由正三角形、正四边形、正五边形时,∠AFB的度数分别为60°,90°,108°,可得出“正n边形”,其它条件不变,则∠AFB度数为
| (n-2)•180° |
| n |
故填:60°;
| (n-2)•180° |
| n |
点评:此题主要考查了正三角边形,正四边形的性质,正五边形的性质与等边三角形与相似三角形的性质,题目综合性很强.

练习册系列答案
相关题目
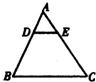 17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
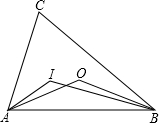 (2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
(2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )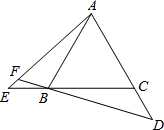 如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是
如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是