题目内容
已知二次函数y=x2-2x-3。
（1）用配方法把该函数化为y=a（x-h）2+k的形式，并写出抛物线y=x2-2x-3的对称轴和顶点坐标；
（2）在直角坐标系中，直接画出抛物线y=x2-2x-3。（注意：关键点要准确，不必写出画图象的过程。）
（3）根据图象回答：①x取什么值时，抛物线在x轴的上方？
②x取什么值时，y的值随x的值的增大而减小？
（2）在直角坐标系中，直接画出抛物线y=x2-2x-3。（注意：关键点要准确，不必写出画图象的过程。）
（3）根据图象回答：①x取什么值时，抛物线在x轴的上方？
②x取什么值时，y的值随x的值的增大而减小？
解：（1）y=x2-2x-3=x2-2x+1-4 =（x-1）2-4
∴抛物线的对称轴是x=1，顶点坐标是（1，-4）；
（2）如图；
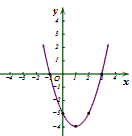
（3）①x<-1或x>3；②x≤1。
练习册系列答案
名校课堂系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．