Question

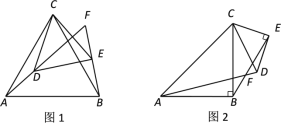
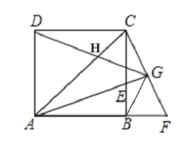
【题目】如图，ABCD为正方形，∠CAB的角平分线交BC于点E，过点C作CF⊥AE交AE的延长线于点G，CF与AB的延长线交于点F，连接BG、DG、与AC相交于点H，则下列结论：①ABECBF；②GF=CG；③BG⊥DG；④，其中正确的是______．

Answer 1

【答案】①②③

【解析】

根据正方形的性质和AG⊥CF，找到边，角相等，然后用ASA证得ABECBF，故①正确；根据条件证明得出ACF是等腰三角形，利用三线合一得出GF=CG，故②正确；延长DG,AB交于点M，证明得出DBM是等腰三角形和G是DM中点，根据三线合一得出BG⊥DG，故③正确；证DCHACE.所以==，所以AE=DH，故④不正确.

∵四边形ABCD为正方形，∴AB=BC，∠ABC=∠CBF=90°

∴∠BAE+∠AEB=90°

∵AG⊥CF

∴∠BCF+∠CEG=90°

∵∠BEA=∠CEG

∴∠BAE=∠BCF

∴ABECBF，故①正确；

∵AG平分∠FAC，AE⊥CF

∴∠CAG=∠FAG，∠AGC=∠AGF=90°

又∵AG=AG，∴ACGAFG.

∴CG=FG，故②正确；

延长DG，AB交于点M，在DCG和MFG中，∠DCG=∠MFG，FG=CG，∠MGF=∠DGC

DCGMFG

∴DG=MG，FM=DC=AB

∴AF=BM．

∵AF=AC，∴BM=AC=BD

∴BG⊥DG，故③正确；

∵∠CDH=∠CAE，∠DCH=∠ACE

∴DCHACE

∴==.

∴AE=DH，故④不正确.

故答案为：①②③