Question

【题目】如图，在正方形ABCD中，E是边CD的中点．

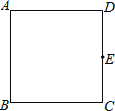
（1）用直尺和圆规作⊙O，使⊙O经过点A、B、E（保留作图痕迹，不写作法）；
（2）若正方形ABCD的边长为2，求（1）中所作⊙O的半径．

Answer 1

【答案】（1）作图见解析；（2）

【解析】

（1）连接AE，分别作出AE，AB的垂直平分线，进而得到交点，即为圆心，求出答案；
（2）根据题意首先得出四边形AFE′D是矩形，进而利用勾股定理得出答案．

（1）如图1所示：
⊙O即为所求．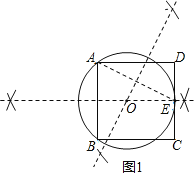

（2）如图2，在（1）中设AB的垂直平分线交AB于点F，交CD于点E′．
则AF=AB=1，∠AFE′=90°，
∵四边形ABCD是正方形，
∴∠FAD=∠D=90°，
∴四边形AFE′D是矩形，
∴E′F=AD=2，DE′=AF=1，
∴点E′与点E重合，
连接OA，设⊙O的半径为r，

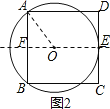
可得OA=OE=r，
∴OF=EF-OE=2-r，
∴在Rt△AOF中，AO2=AF2+OF2，
∴r2=12+（2-r）2，
∴解得：r=，
∴⊙O的半径为．