Question

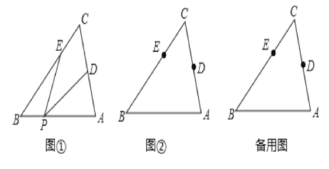
【题目】如图，已知△ABC中，点D、E分别在边AB、AC上，点F在CD上．

（1）若∠AED=∠ACB, ∠DEF= ∠B，求证：EF//AB；

（2）若D、E、F分别是AB、AC、CD的中点，连接BF，若四边形 BDEF的面积为6，试求△ABC的面积．

Answer 1

【答案】（1）详见解析；（2）16

【解析】

（1）根据平行线性质证出∠ADE＝∠DEF，可得EF∥AB；（2）根据三角形中线把三角形面积平分性质求解.

（1）证明：∵∠AED＝∠ACB，∴DE∥BC．∴∠ADE＝∠B．

又∵∠DEF＝∠B，∴∠ADE＝∠DEF，∴EF∥AB．

（2）解：∵点 F 是DC的中点，∴设 S△DEF＝S△CEF＝x，

∵点E是AC的中点，∴S△ADE＝S△CDE＝2x，

∵点D是AB的中点，∴S△BDC＝4x，S△BDF＝2x，∴S 四边形 BDEF＝3x．

∵S 四边形 BDEF＝6，∴3x＝6，∴x＝2，∴S△ABC＝8x＝16．